Note
Click here to download the full example code
Lab: Brain volumes study¶
The study provides the brain volumes of grey matter (gm), white matter (wm) and cerebrospinal fluid) (csf) of 808 anatomical MRI scans.
Manipulate data¶
Set the working directory within a directory called “brainvol”
Create 2 subdirectories: data that will contain downloaded data and reports for results of the analysis.
import os
import os.path
import pandas as pd
import tempfile
import urllib.request
WD = os.path.join(tempfile.gettempdir(), "brainvol")
os.makedirs(WD, exist_ok=True)
#os.chdir(WD)
# use cookiecutter file organization
# https://drivendata.github.io/cookiecutter-data-science/
os.makedirs(os.path.join(WD, "data"), exist_ok=True)
#os.makedirs("reports", exist_ok=True)
Fetch data
Demographic data demo.csv (columns: participant_id, site, group, age, sex) and tissue volume data: group is Control or Patient. site is the recruiting site.
Gray matter volume gm.csv (columns: participant_id, session, gm_vol)
White matter volume wm.csv (columns: participant_id, session, wm_vol)
Cerebrospinal Fluid csf.csv (columns: participant_id, session, csf_vol)
base_url = 'https://github.com/duchesnay/pystatsml/raw/master/datasets/brain_volumes/%s'
data = dict()
for file in ["demo.csv", "gm.csv", "wm.csv", "csf.csv"]:
urllib.request.urlretrieve(base_url % file, os.path.join(WD, "data", file))
# Read all CSV in one line
# dicts = {k: pd.read_csv(os.path.join(WD, "data", "%s.csv" % k))
# for k in ["demo", "gm", "wm", "csf"]}
demo = pd.read_csv(os.path.join(WD, "data", "demo.csv"))
gm = pd.read_csv(os.path.join(WD, "data", "gm.csv"))
wm = pd.read_csv(os.path.join(WD, "data", "wm.csv"))
csf = pd.read_csv(os.path.join(WD, "data", "csf.csv"))
print("tables can be merge using shared columns")
print(gm.head())
Out:
tables can be merge using shared columns
participant_id session gm_vol
0 sub-S1-0002 ses-01 0.67
1 sub-S1-0002 ses-02 0.68
2 sub-S1-0002 ses-03 0.67
3 sub-S1-0004 ses-01 0.89
4 sub-S1-0004 ses-02 0.88
Merge tables according to participant_id
brain_vol = pd.merge(pd.merge(pd.merge(demo, gm), wm), csf)
assert brain_vol.shape == (808, 9)
Drop rows with missing values
brain_vol = brain_vol.dropna()
assert brain_vol.shape == (766, 9)
Compute Total Intra-cranial volume tiv_vol = gm_vol + csf_vol + wm_vol.
brain_vol["tiv_vol"] = brain_vol["gm_vol"] + brain_vol["wm_vol"] + brain_vol["csf_vol"]
Compute tissue fractions gm_f = gm_vol / tiv_vol, wm_f = wm_vol / tiv_vol.
brain_vol["gm_f"] = brain_vol["gm_vol"] / brain_vol["tiv_vol"]
brain_vol["wm_f"] = brain_vol["wm_vol"] / brain_vol["tiv_vol"]
Save in a excel file brain_vol.xlsx
brain_vol.to_excel(os.path.join(WD, "data", "brain_vol.xlsx"),
sheet_name='data', index=False)
Descriptive Statistics¶
Load excel file brain_vol.xlsx
import os
import pandas as pd
import seaborn as sns
import statsmodels.formula.api as smfrmla
import statsmodels.api as sm
brain_vol = pd.read_excel(os.path.join(WD, "data", "brain_vol.xlsx"),
sheet_name='data')
# Round float at 2 decimals when printing
pd.options.display.float_format = '{:,.2f}'.format
Descriptive statistics Most of participants have several MRI sessions (column session) Select on rows from session one “ses-01”
brain_vol1 = brain_vol[brain_vol.session == "ses-01"]
# Check that there are no duplicates
assert len(brain_vol1.participant_id.unique()) == len(brain_vol1.participant_id)
Global descriptives statistics of numerical variables
desc_glob_num = brain_vol1.describe()
print(desc_glob_num)
Out:
age gm_vol wm_vol csf_vol tiv_vol gm_f wm_f
count 244.00 244.00 244.00 244.00 244.00 244.00 244.00
mean 34.54 0.71 0.44 0.31 1.46 0.49 0.30
std 12.09 0.08 0.07 0.08 0.17 0.04 0.03
min 18.00 0.48 0.05 0.12 0.83 0.37 0.06
25% 25.00 0.66 0.40 0.25 1.34 0.46 0.28
50% 31.00 0.70 0.43 0.30 1.45 0.49 0.30
75% 44.00 0.77 0.48 0.37 1.57 0.52 0.31
max 61.00 1.03 0.62 0.63 2.06 0.60 0.36
Global Descriptive statistics of categorical variable
desc_glob_cat = brain_vol1[["site", "group", "sex"]].describe(include='all')
print(desc_glob_cat)
print("Get count by level")
desc_glob_cat = pd.DataFrame({col: brain_vol1[col].value_counts().to_dict()
for col in ["site", "group", "sex"]})
print(desc_glob_cat)
Out:
site group sex
count 244 244 244
unique 7 2 2
top S7 Patient M
freq 65 157 155
Get count by level
site group sex
S7 65.00 nan nan
S5 62.00 nan nan
S8 59.00 nan nan
S3 29.00 nan nan
S4 15.00 nan nan
S1 13.00 nan nan
S6 1.00 nan nan
Patient nan 157.00 nan
Control nan 87.00 nan
M nan nan 155.00
F nan nan 89.00
Remove the single participant from site 6
brain_vol = brain_vol[brain_vol.site != "S6"]
brain_vol1 = brain_vol[brain_vol.session == "ses-01"]
desc_glob_cat = pd.DataFrame({col: brain_vol1[col].value_counts().to_dict()
for col in ["site", "group", "sex"]})
print(desc_glob_cat)
Out:
site group sex
S7 65.00 nan nan
S5 62.00 nan nan
S8 59.00 nan nan
S3 29.00 nan nan
S4 15.00 nan nan
S1 13.00 nan nan
Patient nan 157.00 nan
Control nan 86.00 nan
M nan nan 155.00
F nan nan 88.00
Descriptives statistics of numerical variables per clinical status
desc_group_num = brain_vol1[["group", 'gm_vol']].groupby("group").describe()
print(desc_group_num)
Out:
gm_vol
count mean std min 25% 50% 75% max
group
Control 86.00 0.72 0.09 0.48 0.66 0.71 0.78 1.03
Patient 157.00 0.70 0.08 0.53 0.65 0.70 0.76 0.90
Statistics¶
Objectives:
Site effect of gray matter atrophy
Test the association between the age and gray matter atrophy in the control and patient population independently.
Test for differences of atrophy between the patients and the controls
Test for interaction between age and clinical status, ie: is the brain atrophy process in patient population faster than in the control population.
The effect of the medication in the patient population.
import statsmodels.api as sm
import statsmodels.formula.api as smfrmla
import scipy.stats
import seaborn as sns
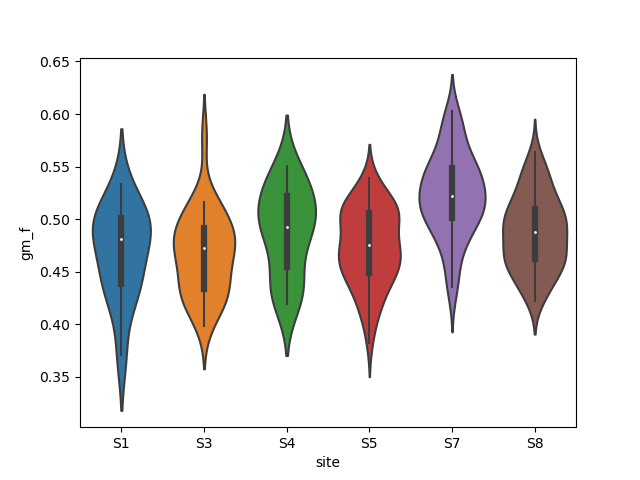
1 Site effect on Grey Matter atrophy
The model is Oneway Anova gm_f ~ site The ANOVA test has important assumptions that must be satisfied in order for the associated p-value to be valid.
The samples are independent.
Each sample is from a normally distributed population.
The population standard deviations of the groups are all equal. This property is known as homoscedasticity.
Plot
sns.violinplot(x="site", y="gm_f", data=brain_vol1)
# sns.violinplot(x="site", y="wm_f", data=brain_vol1)
Out:
<AxesSubplot:xlabel='site', ylabel='gm_f'>
Stats with scipy
fstat, pval = scipy.stats.f_oneway(*[brain_vol1.gm_f[brain_vol1.site == s]
for s in brain_vol1.site.unique()])
print("Oneway Anova gm_f ~ site F=%.2f, p-value=%E" % (fstat, pval))
Out:
Oneway Anova gm_f ~ site F=14.82, p-value=1.188136E-12
Stats with statsmodels
anova = smfrmla.ols("gm_f ~ site", data=brain_vol1).fit()
# print(anova.summary())
print("Site explains %.2f%% of the grey matter fraction variance" %
(anova.rsquared * 100))
print(sm.stats.anova_lm(anova, typ=2))
Out:
Site explains 23.82% of the grey matter fraction variance
sum_sq df F PR(>F)
site 0.11 5.00 14.82 0.00
Residual 0.35 237.00 nan nan
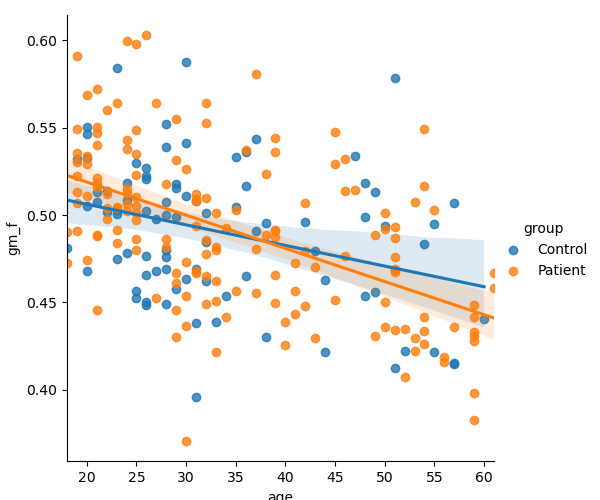
2. Test the association between the age and gray matter atrophy in the control and patient population independently.
Plot
sns.lmplot(x="age", y="gm_f", hue="group", data=brain_vol1)
brain_vol1_ctl = brain_vol1[brain_vol1.group == "Control"]
brain_vol1_pat = brain_vol1[brain_vol1.group == "Patient"]
Stats with scipy
print("--- In control population ---")
beta, beta0, r_value, p_value, std_err = \
scipy.stats.linregress(x=brain_vol1_ctl.age, y=brain_vol1_ctl.gm_f)
print("gm_f = %f * age + %f" % (beta, beta0))
print("Corr: %f, r-squared: %f, p-value: %f, std_err: %f"\
% (r_value, r_value**2, p_value, std_err))
print("--- In patient population ---")
beta, beta0, r_value, p_value, std_err = \
scipy.stats.linregress(x=brain_vol1_pat.age, y=brain_vol1_pat.gm_f)
print("gm_f = %f * age + %f" % (beta, beta0))
print("Corr: %f, r-squared: %f, p-value: %f, std_err: %f"\
% (r_value, r_value**2, p_value, std_err))
print("Decrease seems faster in patient than in control population")
Out:
--- In control population ---
gm_f = -0.001181 * age + 0.529829
Corr: -0.325122, r-squared: 0.105704, p-value: 0.002255, std_err: 0.000375
--- In patient population ---
gm_f = -0.001899 * age + 0.556886
Corr: -0.528765, r-squared: 0.279592, p-value: 0.000000, std_err: 0.000245
Decrease seems faster in patient than in control population
Stats with statsmodels
print("--- In control population ---")
lr = smfrmla.ols("gm_f ~ age", data=brain_vol1_ctl).fit()
print(lr.summary())
print("Age explains %.2f%% of the grey matter fraction variance" %
(lr.rsquared * 100))
print("--- In patient population ---")
lr = smfrmla.ols("gm_f ~ age", data=brain_vol1_pat).fit()
print(lr.summary())
print("Age explains %.2f%% of the grey matter fraction variance" %
(lr.rsquared * 100))
Out:
--- In control population ---
OLS Regression Results
===============================================================================
Dep. Variable: gm_f R-squared: 0.106
Model: OLS Adj. R-squared: 0.095
Method: Least Squares F-statistic: 9.929
Date: ven., 08 janv. 2021 Prob (F-statistic): 0.00226
Time: 16:12:34 Log-Likelihood: 159.34
No. Observations: 86 AIC: -314.7
Df Residuals: 84 BIC: -309.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.5298 0.013 40.350 0.000 0.504 0.556
age -0.0012 0.000 -3.151 0.002 -0.002 -0.000
==============================================================================
Omnibus: 0.946 Durbin-Watson: 1.628
Prob(Omnibus): 0.623 Jarque-Bera (JB): 0.782
Skew: 0.233 Prob(JB): 0.676
Kurtosis: 2.962 Cond. No. 111.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Age explains 10.57% of the grey matter fraction variance
--- In patient population ---
OLS Regression Results
===============================================================================
Dep. Variable: gm_f R-squared: 0.280
Model: OLS Adj. R-squared: 0.275
Method: Least Squares F-statistic: 60.16
Date: ven., 08 janv. 2021 Prob (F-statistic): 1.09e-12
Time: 16:12:34 Log-Likelihood: 289.38
No. Observations: 157 AIC: -574.8
Df Residuals: 155 BIC: -568.7
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.5569 0.009 60.817 0.000 0.539 0.575
age -0.0019 0.000 -7.756 0.000 -0.002 -0.001
==============================================================================
Omnibus: 2.310 Durbin-Watson: 1.325
Prob(Omnibus): 0.315 Jarque-Bera (JB): 1.854
Skew: 0.230 Prob(JB): 0.396
Kurtosis: 3.268 Cond. No. 111.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Age explains 27.96% of the grey matter fraction variance
Before testing for differences of atrophy between the patients ans the controls Preliminary tests for age x group effect (patients would be older or younger than Controls)
Plot
sns.violinplot(x="group", y="age", data=brain_vol1)
Out:
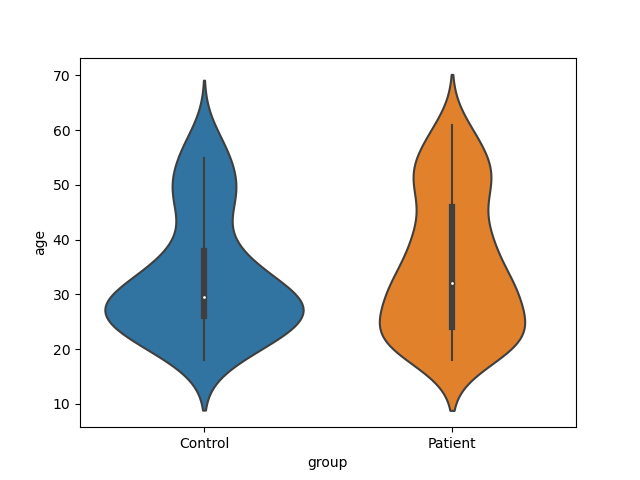
<AxesSubplot:xlabel='group', ylabel='age'>
Stats with scipy
print(scipy.stats.ttest_ind(brain_vol1_ctl.age, brain_vol1_pat.age))
Out:
Ttest_indResult(statistic=-1.2155557697674162, pvalue=0.225343592508479)
Stats with statsmodels
print(smfrmla.ols("age ~ group", data=brain_vol1).fit().summary())
print("No significant difference in age between patients and controls")
Out:
OLS Regression Results
===============================================================================
Dep. Variable: age R-squared: 0.006
Model: OLS Adj. R-squared: 0.002
Method: Least Squares F-statistic: 1.478
Date: ven., 08 janv. 2021 Prob (F-statistic): 0.225
Time: 16:12:34 Log-Likelihood: -949.69
No. Observations: 243 AIC: 1903.
Df Residuals: 241 BIC: 1910.
Df Model: 1
Covariance Type: nonrobust
====================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------
Intercept 33.2558 1.305 25.484 0.000 30.685 35.826
group[T.Patient] 1.9735 1.624 1.216 0.225 -1.225 5.172
==============================================================================
Omnibus: 35.711 Durbin-Watson: 2.096
Prob(Omnibus): 0.000 Jarque-Bera (JB): 20.726
Skew: 0.569 Prob(JB): 3.16e-05
Kurtosis: 2.133 Cond. No. 3.12
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
No significant difference in age between patients and controls
Preliminary tests for sex x group (more/less males in patients than in Controls)
crosstab = pd.crosstab(brain_vol1.sex, brain_vol1.group)
print("Obeserved contingency table")
print(crosstab)
chi2, pval, dof, expected = scipy.stats.chi2_contingency(crosstab)
print("Chi2 = %f, pval = %f" % (chi2, pval))
print("No significant difference in sex between patients and controls")
Out:
Obeserved contingency table
group Control Patient
sex
F 33 55
M 53 102
Chi2 = 0.143253, pval = 0.705068
No significant difference in sex between patients and controls
3. Test for differences of atrophy between the patients and the controls
print(sm.stats.anova_lm(smfrmla.ols("gm_f ~ group", data=brain_vol1).fit(),
typ=2))
print("No significant difference in atrophy between patients and controls")
Out:
sum_sq df F PR(>F)
group 0.00 1.00 0.01 0.92
Residual 0.46 241.00 nan nan
No significant difference in atrophy between patients and controls
This model is simplistic we should adjust for age and site
print(sm.stats.anova_lm(smfrmla.ols(
"gm_f ~ group + age + site", data=brain_vol1).fit(), typ=2))
print("No significant difference in GM between patients and controls")
Out:
sum_sq df F PR(>F)
group 0.00 1.00 1.82 0.18
site 0.11 5.00 19.79 0.00
age 0.09 1.00 86.86 0.00
Residual 0.25 235.00 nan nan
No significant difference in GM between patients and controls
Observe age effect
4. Test for interaction between age and clinical status, ie: is the brain atrophy process in patient population faster than in the control population.
ancova = smfrmla.ols("gm_f ~ group:age + age + site", data=brain_vol1).fit()
print(sm.stats.anova_lm(ancova, typ=2))
print("= Parameters =")
print(ancova.params)
print("%.3f%% of grey matter loss per year (almost %.1f%% per decade)" %
(ancova.params.age * 100, ancova.params.age * 100 * 10))
print("grey matter loss in patients is accelerated by %.3f%% per decade" %
(ancova.params['group[T.Patient]:age'] * 100 * 10))
Out:
sum_sq df F PR(>F)
site 0.11 5.00 20.28 0.00
age 0.10 1.00 89.37 0.00
group:age 0.00 1.00 3.28 0.07
Residual 0.25 235.00 nan nan
= Parameters =
Intercept 0.52
site[T.S3] 0.01
site[T.S4] 0.03
site[T.S5] 0.01
site[T.S7] 0.06
site[T.S8] 0.02
age -0.00
group[T.Patient]:age -0.00
dtype: float64
-0.148% of grey matter loss per year (almost -1.5% per decade)
grey matter loss in patients is accelerated by -0.232% per decade
Total running time of the script: ( 0 minutes 3.007 seconds)