Linear Models for Regression¶
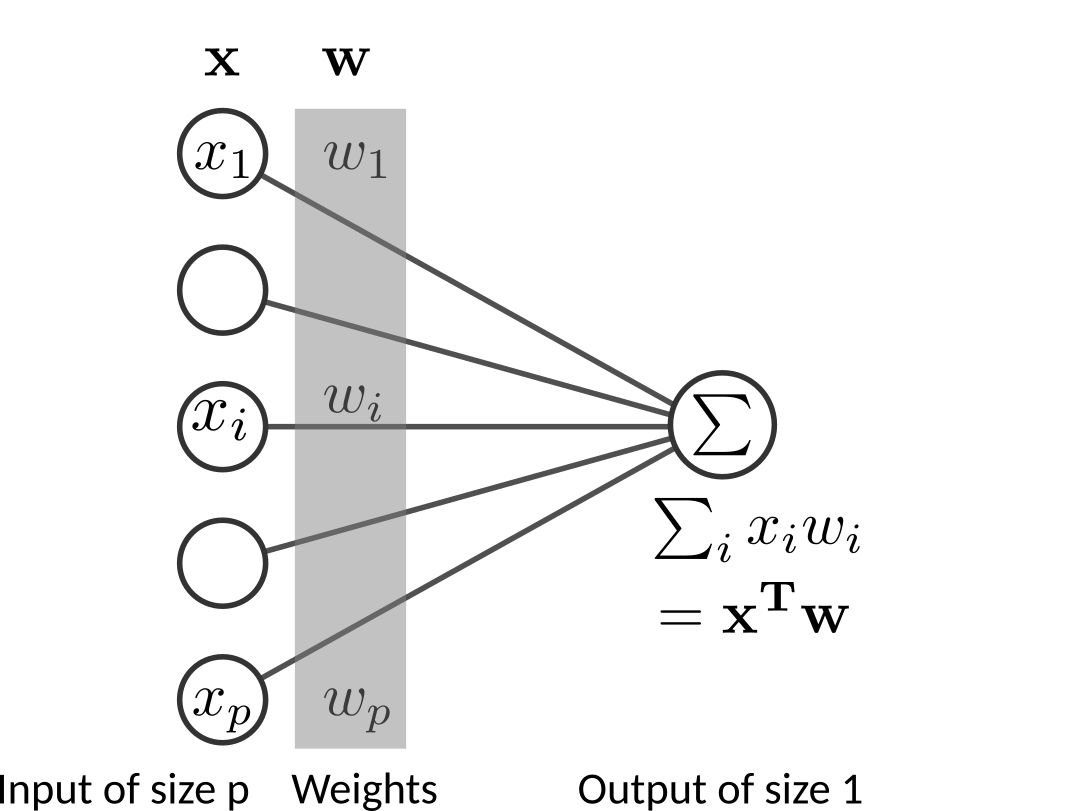
Linear regression¶
Minimizing the Sum of Squared Errors (SSE) Loss¶
A linear model assumes a linear relationship between input features of observation \(i\) \(\mathbf{x}_i \in \mathbb{R}^{P}\) and an output \(y \in \mathrm{R}\) using:
where \(\boldsymbol{\varepsilon}_i \in \mathrm{R}\) is the residual or the error of the prediction. \(\mathbf{w}\) is the weight vector (model’s parameters) of coefficients. \(\mathbf{w}\) is found by minimizing an objective function, which is the loss function, \(L(\mathbf{w})\), i.e. the error measured on the data. This error is the sum of squared errors (SSE) loss:
The equivalent matrix notation is:
where \(\mathbf{X}\) be the \(N \times P\) matrix with each row an input vector and similarly let \(\mathbf{y}\) the \(N\)-dimensional vector of outputs.
The loss is given by
Minimizing the SSE is the Ordinary Least Square OLS regression as objective function. which is a simple ordinary least squares (OLS) minimization whose analytic solution is:
The solution could also be found using gradient descent using the gradient of the loss:
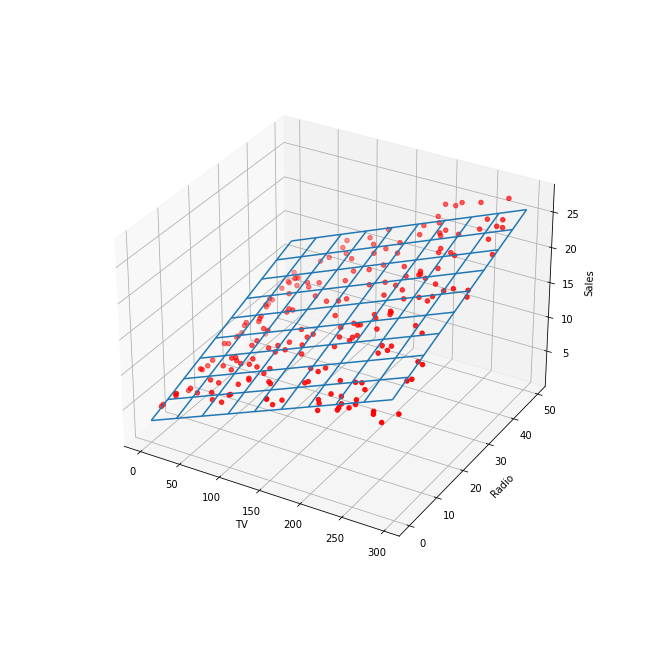
Linear regression of Advertising.csv dataset with TV and Radio
advertising as input features and Sales as target. The linear model that
minimizes the MSE is a plan (2 input features) defined as: Sales = 0.05
TV + .19 Radio + 3:
Linear regression¶
Linear regression with scikit-learn¶
Scikit-learn offers many models for supervised learning, and they all follow the same Application Programming Interface (API), namely:
est = Estimator()
est.fit(X, y)
predictions = est.predict(X)
import numpy as np
import pandas as pd
# Plot
import matplotlib.pyplot as plt
import seaborn as sns
# Plot parameters
plt.style.use('seaborn-v0_8-whitegrid')
fig_w, fig_h = plt.rcParams.get('figure.figsize')
plt.rcParams['figure.figsize'] = (fig_w, fig_h * .5)
from sklearn import datasets
import sklearn.linear_model as lm
import sklearn.metrics as metrics
# Dataset with some correlation
X, y, coef = datasets.make_regression(n_samples=100, n_features=10,
n_informative=5, random_state=0,
effective_rank=3, coef=True)
lr = lm.LinearRegression().fit(X, y)
Regularization using penalization of coefficients¶
Regarding linear models, overfitting generally leads to excessively complex solutions (coefficient vectors), accounting for noise or spurious correlations within predictors. Regularization aims to alleviate this phenomenon by constraining (biasing or reducing) the capacity of the learning algorithm in order to promote simple solutions. Regularization penalizes “large” solutions forcing the coefficients to be small, i.e. to shrink them toward zeros.
The objective function \(J(\mathbf{w})\) to minimize with respect to \(\mathbf{w}\) is composed of a loss function \(L(\mathbf{w})\) for goodness-of-fit and a penalty term \(\Omega(\mathbf{w})\) (regularization to avoid overfitting). This is a trade-off where the respective contribution of the loss and the penalty terms is controlled by the regularization parameter \(\lambda\).
Therefore the loss function \(L(\mathbf{w})\) is combined with a penalty function \(\Omega(\mathbf{w})\) leading to the general form:
The respective contribution of the loss and the penalty is controlled by the regularization hyper-parameter \(\lambda\).
Regularization exploits Occam’s razor is a principle
Occam’s razor is a principle stating that, among competing hypotheses, the one with the fewest assumptions should be selected. This is also known as the principle of parsimony, favoring simpler explanations or models when possible. In machine learning, this translates to preferring models with similar loss but lower complexity.
Ridge Regression (\(\ell_2\) or L2 regularization)¶
Penalty: \(\Omega(\mathbf{w}) = \|\mathbf{w}\|_2^2 = \sum_{j} w_j^2\)
Objective function:
\[\text{Ridge}(\mathbf{w}) = \sum_i^N (y_i - \mathbf{x}_i^\top\mathbf{w})^2 + \lambda \|\mathbf{w}\|_2^2\]Effect: Shrinks all coefficients smoothly towards zero, but does not enforce sparsity (no coefficients become exactly zero).
The gradient of the loss:
\[\partial\frac{L(\mathbf{w}, \mathbf{X}, \mathbf{y})}{\partial\mathbf{w}} = 2 (\sum_i \mathbf{x}_i (\mathbf{x}_i \cdot \mathbf{w} - y_i) + \lambda \mathbf{w})\]
Numerical Interpretation¶
Using the matrix notation, he Ridge objective function can be rewritten as
The \(\mathbf{w}\) that minimizes \(F_{Ridge}(\mathbf{w})\) can be found by the following derivation:
The solution adds a positive constant to the diagonal of \(\mathbf{X}^\top\mathbf{X}\) before inversion. This makes the problem nonsingular, even if \(\mathbf{X}^\top\mathbf{X}\) is not of full rank, and was the main motivation behind ridge regression.
Increasing \(\lambda\) shrinks the \(\mathbf{w}\) coefficients toward 0.
Solutions with large coefficients become unattractive.
Lasso Regression (\(\ell_1\) or L1 regularization)¶
Penalty: \(\Omega(\mathbf{w}) = \|\mathbf{w}\|_1 = \sum_{j} |w_j|\)
Objective function:
\[\text{Lasso}(\mathbf{w}) = \sum_i^N (y_i - \mathbf{x}_i^\top\mathbf{w})^2 + \lambda \sum_{j} |w_j|\]Effect: Promotes sparsity, i.e., forces some coefficients to be exactly zero, ie. performs feature selection.
No closed-form solution, It is convex but not differentiable. Requires specific optimization algorithms, such as the fast iterative shrinkage-thresholding algorithm (FISTA): Amir Beck and Marc Teboulle, A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems SIAM J. Imaging Sci., 2009.
Geometric interpretation¶
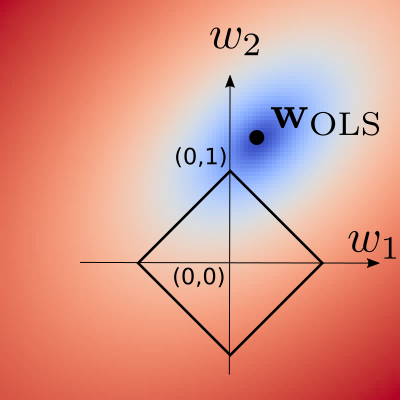
Sparsity of L1 norm¶
Elastic Net¶
Penalty: Combination of L1 and L2: \(\Omega(\mathbf{w}) = \alpha \|\mathbf{w}\|_1 + (1 - \alpha) \|\mathbf{w}\|_2^2\) where \(\alpha \in [0, 1]\) controls the mix of Lasso and Ridge.
Effect: Balances sparsity (L1) and stability (L2), especially useful when features are correlated.
The Elastic-net estimator combines the \(\ell_1\) and \(\ell_2\) penalties, and results in the problem to
where \(\alpha\) acts as a global penalty and \(\rho\) as an \(\ell_1 / \ell_2\) ratio.
Rational¶
If there are groups of highly correlated variables, Lasso tends to arbitrarily select only one from each group. These models are difficult to interpret because covariates that are strongly associated with the outcome are not included in the predictive model. Conversely, the elastic net encourages a grouping effect, where strongly correlated predictors tend to be in or out of the model together.
Studies on real world data and simulation studies show that the elastic net often outperforms the lasso, while enjoying a similar sparsity of representation.
Penalization: summary and and Application with scikit-learn¶
Summary¶
Method |
Penalty Type |
Promotes Sparsity |
Handles M ulticollinearity |
Closed-Form Solution |
|---|---|---|---|---|
Ridge |
L2: :m ath:sum _j w_j^2 |
No |
Yes |
Yes |
Lasso |
L1: :mat h:`sum_j
|
Yes |
No (can be unstable) |
No |
E lastic Net |
L1 + L2 |
Yes (less than Lasso) |
Yes |
No |
Effect on problems with increasing dimension¶
The next figure shows the predicted performance (r-squared) on train and test sets with an increasing number of input features. The number of predictive features is always 10% of the total number of input features. Therefore, the signal to noise ratio (SNR) increases by increasing the number of input features. The performances on the training set rapidly reach 100% (R2=1). However, the performance on the test set decreases with the increase of the input dimensionality. The difference between the train and test performances (blue shaded region) depicts the overfitting phenomena. Regularization using penalties of the coefficient vector norm greatly limits the overfitting phenomena.
Effect on solution finding¶
The ridge penalty shrinks the coefficients toward zero. The figure illustrates: the OLS solution on the left. The \(\ell_1\) and \(\ell_2\) penalties in the middle pane. The penalized OLS in the right pane. The right pane shows how the penalties shrink the coefficients toward zero. The black points are the minimum found in each case, and the white points represents the true solution used to generate the data.
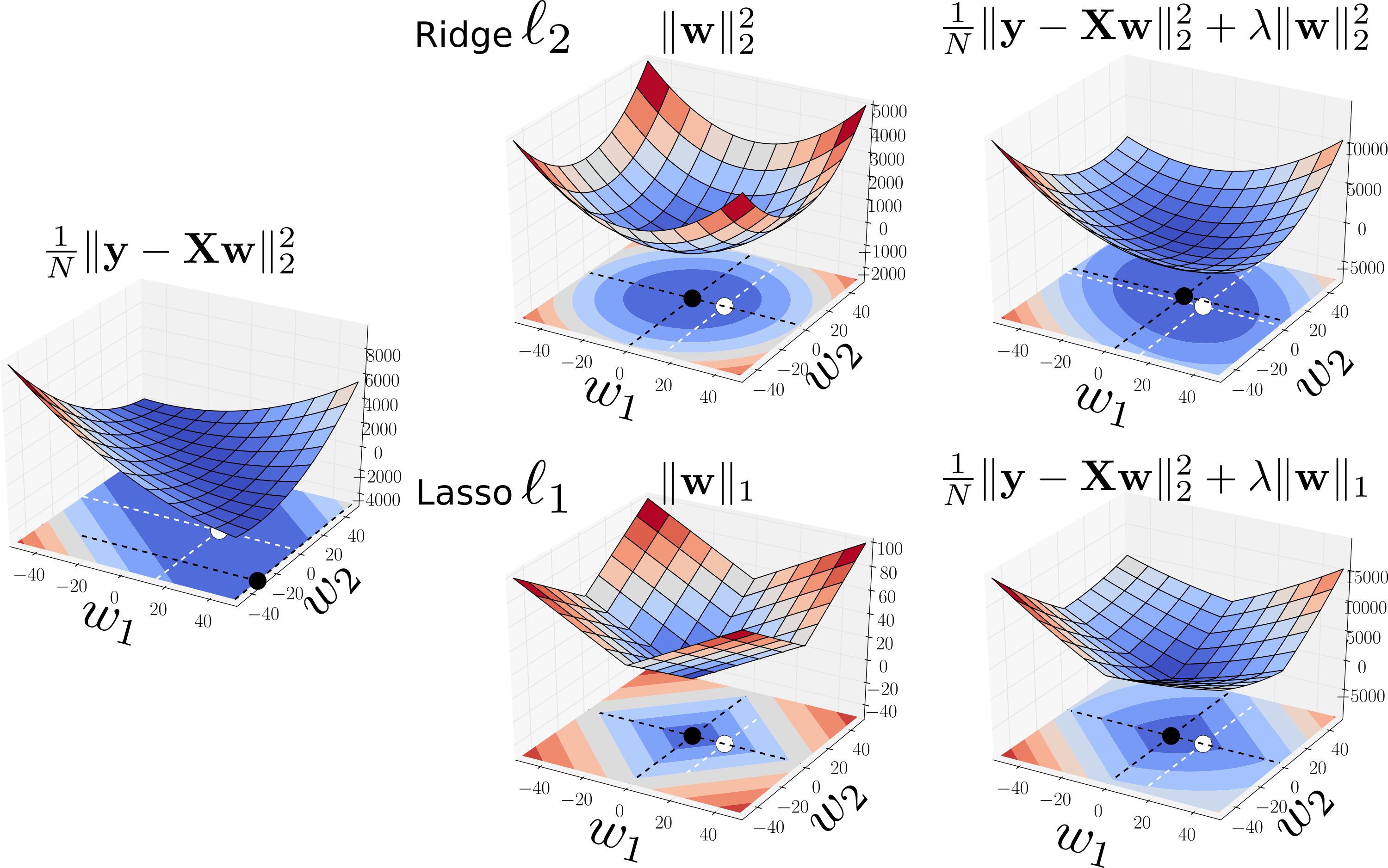
\(\ell_1\) and \(\ell_2\) shrinkages¶
Application with scikit-learn¶
l2 = lm.Ridge(alpha=10).fit(X, y) # lambda is alpha!
l1 = lm.Lasso(alpha=.1).fit(X, y) # lambda is alpha !
l1l2 = lm.ElasticNet(alpha=.1, l1_ratio=.9).fit(X, y)
print(pd.DataFrame(np.vstack((coef, lr.coef_, l2.coef_, l1.coef_, l1l2.coef_)),
index=['True', 'lr', 'l2', 'l1', 'l1l2']).round(2))
0 1 2 3 4 5 6 7 8 9
True 28.49 0.00 13.17 0.00 48.97 70.44 39.70 0.00 0.00 0.00
lr 28.49 0.00 13.17 0.00 48.97 70.44 39.70 0.00 0.00 -0.00
l2 1.03 0.21 0.93 -0.32 1.82 1.57 2.10 -1.14 -0.84 -1.02
l1 0.00 -0.00 0.00 -0.00 24.40 25.16 25.36 -0.00 -0.00 -0.00
l1l2 0.78 0.00 0.51 -0.00 7.20 5.71 8.95 -1.38 -0.00 -0.40
Sparsity of the \(\ell_1\) norm¶
Occam’s razor¶
Occam’s razor (also written as Ockham’s razor, and lex parsimoniae in Latin, which means law of parsimony) is a problem solving principle attributed to William of Ockham (1287-1347), who was an English Franciscan friar and scholastic philosopher and theologian. The principle can be interpreted as stating that among competing hypotheses, the one with the fewest assumptions should be selected.
Principle of parsimony¶
The simplest of two competing theories is to be preferred. Definition of parsimony: Economy of explanation in conformity with Occam’s razor.
Among possible models with similar loss, choose the simplest one:
Choose the model with the smallest coefficient vector, i.e. smallest \(\ell_2\) (\(\|\mathbf{w}\|_2\)) or \(\ell_1\) (\(\|\mathbf{w}\|_1\)) norm of \(\mathbf{w}\), i.e. \(\ell_2\) or \(\ell_1\) penalty. See also bias-variance tradeoff.
Choose the model that uses the smallest number of predictors. In other words, choose the model that has many predictors with zero weights. Two approaches are available to obtain this: (i) Perform a feature selection as a preprocessing prior to applying the learning algorithm, or (ii) embed the feature selection procedure within the learning process.
Regression performance evaluation metrics: R-squared, MSE and MAE¶
Common regression Scikit-learn Metrics are:
\(R^2\) : R-squared
MSE: Mean Squared Error
MAE: Mean Absolute Error
R-squared¶
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. We will consider the explained variance also known as the coefficient of determination, denoted \(R^2\) pronounced R-squared.
The total sum of squares, \(SS_\text{tot}\) is the sum of the sum of squares explained by the regression, \(SS_\text{reg}\), plus the sum of squares of residuals unexplained by the regression, \(SS_\text{res}\), also called the SSE, i.e. such that
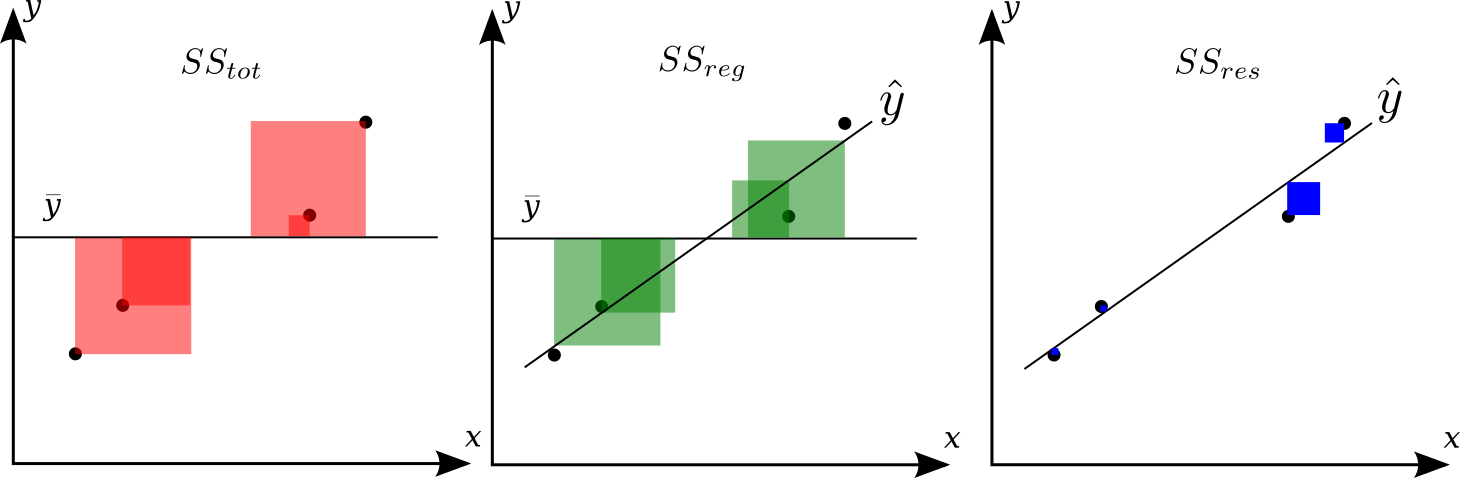
title¶
The mean of \(y\) is
The total sum of squares is the total squared sum of deviations from the mean of \(y\), i.e.
The regression sum of squares, also called the explained sum of squares:
where \(\hat{y}_i = \beta x_i + \beta_0\) is the estimated value of salary \(\hat{y}_i\) given a value of experience \(x_i\).
The sum of squares of the residuals (SSE, Sum Squared Error), also called the residual sum of squares (RSS) is:
\(R^2\) is the explained sum of squares of errors. It is the variance explain by the regression divided by the total variance, i.e.
Test
Let \(\hat{\sigma}^2 = SS_\text{res} / (n-2)\) be an estimator of the variance of \(\epsilon\). The \(2\) in the denominator stems from the 2 estimated parameters: intercept and coefficient.
Unexplained variance: \(\frac{SS_\text{res}}{\hat{\sigma}^2} \sim \chi_{n-2}^2\)
Explained variance: \(\frac{SS_\text{reg}}{\hat{\sigma}^2} \sim \chi_{1}^2\). The single degree of freedom comes from the difference between \(\frac{SS_\text{tot}}{\hat{\sigma}^2} (\sim \chi^2_{n-1})\) and \(\frac{SS_\text{res}}{\hat{\sigma}^2} (\sim \chi_{n-2}^2)\), i.e. \((n-1) - (n-2)\) degree of freedom.
The Fisher statistics of the ratio of two variances:
Using the \(F\)-distribution, compute the probability of observing a value greater than \(F\) under \(H_0\), i.e.: \(P(x > F|H_0)\), i.e. the survival function \((1 - \text{Cumulative Distribution Function})\) at \(x\) of the given \(F\)-distribution.
import sklearn.metrics as metrics
from sklearn.model_selection import train_test_split
X, y = datasets.make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1)
lr = lm.LinearRegression()
lr.fit(X_train, y_train)
yhat = lr.predict(X_test)
r2 = metrics.r2_score(y_test, yhat)
mse = metrics.mean_squared_error(y_test, yhat)
mae = metrics.mean_absolute_error(y_test, yhat)
print("r2: %.3f, mae: %.3f, mse: %.3f" % (r2, mae, mse))
r2: 0.053, mae: 71.712, mse: 7866.759
In pure numpy:
res = y_test - lr.predict(X_test)
y_mu = np.mean(y_test)
ss_tot = np.sum((y_test - y_mu) ** 2)
ss_res = np.sum(res ** 2)
r2 = (1 - ss_res / ss_tot)
mse = np.mean(res ** 2)
mae = np.mean(np.abs(res))
print("r2: %.3f, mae: %.3f, mse: %.3f" % (r2, mae, mse))
r2: 0.053, mae: 71.712, mse: 7866.759