Note
Click here to download the full example code
Resampling methods¶
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
import sklearn.linear_model as lm
from sklearn.model_selection import train_test_split, KFold, PredefinedSplit
from sklearn.model_selection import cross_val_score, GridSearchCV
import sklearn.metrics as metrics
X, y = datasets.make_regression(n_samples=100, n_features=100,
n_informative=10, random_state=42)
Train, validation and test sets¶
Machine learning algorithms overfit taining data. Predictive performances MUST be evaluated on independant hold-out dataset.
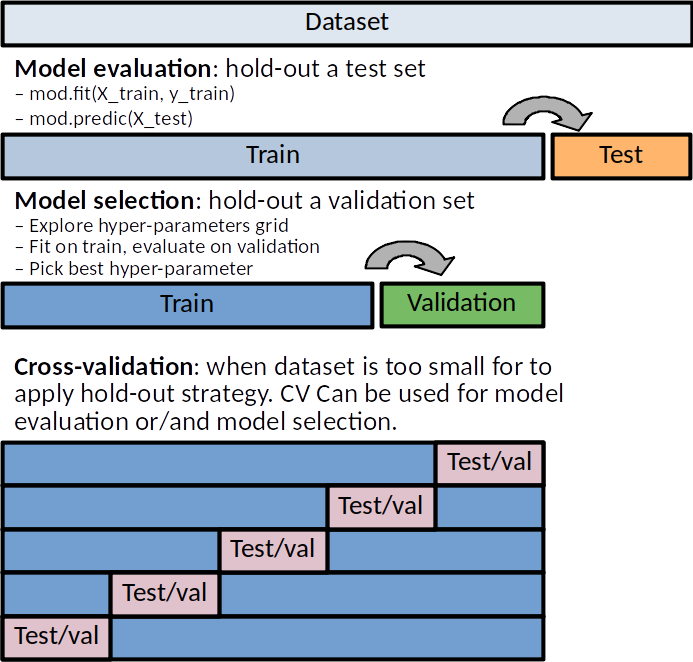
Training dataset: Dataset used to fit the model (set the model parameters like weights). The training error can be easily calculated by applying the statistical learning method to the observations used in its training. But because of overfitting, the training error rate can dramatically underestimate the error that would be obtained on new samples.
Validation dataset: Dataset used to provide an unbiased evaluation of a model fit on the training dataset while tuning model hyperparameters, ie. model selection. The validation error is the average error that results from a learning method to predict the response on a new (validation) samples that is, on samples that were not used in training the method.
Test dataset: Dataset used to provide an unbiased evaluation of a final model fitted on the training dataset. It is only used once a model is completely trained (using the train and validation sets).
What is the Difference Between Test and Validation Datasets? by [Jason Brownlee](https://machinelearningmastery.com/difference-test-validation-datasets/)
Thus the original dataset is generally split in a training, validation and a test data sets. Large training+validation set (80%) small test set (20%) might provide a poor estimation of the predictive performances (same argument stands for train vs validation samples). On the contrary, large test set and small training set might produce a poorly estimated learner. This is why, on situation where we cannot afford such split, cross-validation scheme can be use for model selection or/and for model evaluation.
If sample size is limited, train/validation/test split may not be possible. Cross Validation (CV) (see below) can be used to replace:
Outer (train/test) split of model evaluation.
Inner train/validation split of model selection (more frequent situation).
Inner and outer splits, leading to two nested CV.
Split dataset in train/test sets for model evaluation¶
X_train, X_test, y_train, y_test =\
train_test_split(X, y, test_size=0.25, shuffle=True, random_state=42)
mod = lm.Ridge(alpha=10)
mod.fit(X_train, y_train)
y_pred_test = mod.predict(X_test)
print("Test R2: %.2f" % metrics.r2_score(y_test, y_pred_test))
Out:
Test R2: 0.74
Train/validation/test splits: model selection and model evaluation¶
The Grid search procedure (GridSearchCV) performs a model selection of the best hyper-parameters \(\alpha\) over a grid of possible values. Train set is “splitted (inner split) into train/validation sets.
Model selection with grid search procedure:
Fit the learner (ie. estimate parameters \(\mathbf{\Omega}_k\)) on training set: \(\mathbf{X}_{train}, \mathbf{y}_{train} \rightarrow f_{\alpha_k, \mathbf{\Omega}_k}(.)\)
Evaluate the model on the validation set and keep the hyper-parameter(s) that minimises the error measure \(\alpha_* = \arg \min L(f_{\alpha_k, \mathbf{\Omega}_k}(\mathbf{X}_{val}), \mathbf{y}_{val})\)
Refit the learner on all training + validation data, \(\mathbf{X}_{train \cup val}, \mathbf{y}_{train \cup val}\), using the best hyper parameters (\(\alpha_*\)): \(\rightarrow f_{\alpha_*, \mathbf{\Omega}_*}(.)\)
Model evaluation: on the test set: \(L(f_{\alpha_*, \mathbf{\Omega}_*}(\mathbf{X}_{test}), \mathbf{y}_{test})\)
train_idx, validation_idx = train_test_split(np.arange(X_train.shape[0]),
test_size=0.25, shuffle=True,
random_state=42)
split_inner = PredefinedSplit(test_fold=validation_idx)
print("Train set size: %i" % X_train[train_idx].shape[0])
print("Validation set size: %i" % X_train[validation_idx].shape[0])
print("Test set size: %i" % X_test.shape[0])
lm_cv = GridSearchCV(lm.Ridge(), {'alpha': 10. ** np.arange(-3, 3)},
cv=split_inner, n_jobs=5)
# Fit, indluding model selection with internal Train/validation split
lm_cv.fit(X_train, y_train)
# Predict
y_pred_test = lm_cv.predict(X_test)
print("Test R2: %.2f" % metrics.r2_score(y_test, y_pred_test))
Out:
Train set size: 56
Validation set size: 19
Test set size: 25
Test R2: 0.80
Cross-Validation (CV)¶
If sample size is limited, train/validation/test split may not be possible. Cross Validation (CV) can be used to replace train/validation split and/or train+validation / test split.
Cross-Validation scheme randomly divides the set of observations into K groups, or folds, of approximately equal size. The first fold is treated as a validation set, and the method \(f()\) is fitted on the remaining union of K - 1 folds: (\(f(\boldsymbol{X}_{-K}, \boldsymbol{y}_{-K})\)). The measure of performance (the score function \(\mathcal{S}\)), either a error measure or an correct prediction measure is an average of a loss error or correct prediction measure, noted \(\mathcal{L}\), between a true target value and the predicted target value. The score function is evaluated of the on the observations in the held-out fold. For each sample i we consider the model estimated \(f(\boldsymbol{X}_{-k(i)}, \boldsymbol{y}_{-k(i)}\) on the data set without the group k that contains i noted -k(i). This procedure is repeated K times; each time, a different group of observations is treated as a test set. Then we compare the predicted value (\(f_{-k(i)}(\boldsymbol{x}_i) = \hat{y_i})\) with true value \(y_i\) using a Error or Loss function \(\mathcal{L}(y, \hat{y})\).
For 10-fold we can either average over 10 values (Macro measure) or concatenate the 10 experiments and compute the micro measures.
Two strategies [micro vs macro estimates](https://stats.stackexchange.com/questions/34611/meanscores-vs-scoreconcatenation-in-cross-validation):
Micro measure: average(individual scores): compute a score \(\mathcal{S}\) for each sample and average over all samples. It is simillar to average score(concatenation): an averaged score computed over all concatenated samples.
Macro measure mean(CV scores) (the most commonly used method): compute a score \(\mathcal{S}\) on each each fold k and average accross folds:
These two measures (an average of average vs. a global average) are generaly similar. They may differ slightly is folds are of different sizes. This validation scheme is known as the K-Fold CV. Typical choices of K are 5 or 10, [Kohavi 1995]. The extreme case where K = N is known as leave-one-out cross-validation, LOO-CV.
CV for regression¶
Usually the error function \(\mathcal{L}()\) is the r-squared score. However other function (MAE, MSE) can be used.
CV with explicit loop:
from sklearn.model_selection import KFold
estimator = lm.Ridge(alpha=10)
cv = KFold(n_splits=5, shuffle=True, random_state=42)
r2_train, r2_test = list(), list()
for train, test in cv.split(X):
estimator.fit(X[train, :], y[train])
r2_train.append(metrics.r2_score(y[train], estimator.predict(X[train, :])))
r2_test.append(metrics.r2_score(y[test], estimator.predict(X[test, :])))
print("Train r2:%.2f" % np.mean(r2_train))
print("Test r2:%.2f" % np.mean(r2_test))
Out:
Train r2:0.99
Test r2:0.67
Scikit-learn provides user-friendly function to perform CV:
cross_val_score(): single metric
from sklearn.model_selection import cross_val_score
scores = cross_val_score(estimator=estimator, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
cv = KFold(n_splits=5, shuffle=True, random_state=42)
scores = cross_val_score(estimator=estimator, X=X, y=y, cv=cv)
print("Test r2:%.2f" % scores.mean())
Out:
Test r2:0.73
Test r2:0.67
cross_validate(): multi metric, + time, etc.
from sklearn.model_selection import cross_validate
scores = cross_validate(estimator=mod, X=X, y=y, cv=cv,
scoring=['r2', 'neg_mean_absolute_error'])
print("Test R2:%.2f; MAE:%.2f" % (scores['test_r2'].mean(),
-scores['test_neg_mean_absolute_error'].mean()))
Out:
Test R2:0.67; MAE:55.27
CV for classification: stratifiy for the target label¶
With classification problems it is essential to sample folds where each
set contains approximately the same percentage of samples of each target
class as the complete set. This is called stratification.
In this case, we will use StratifiedKFold with is a variation of
k-fold which returns stratified folds.
Usually the error function \(L()\) are, at least, the sensitivity
and the specificity. However other function could be used.
CV with explicit loop:
from sklearn.model_selection import StratifiedKFold
X, y = datasets.make_classification(n_samples=100, n_features=100, shuffle=True,
n_informative=10, random_state=42)
mod = lm.LogisticRegression(C=1, solver='lbfgs')
cv = StratifiedKFold(n_splits=5)
# Lists to store scores by folds (for macro measure only)
bacc, auc = [], []
for train, test in cv.split(X, y):
mod.fit(X[train, :], y[train])
bacc.append(metrics.roc_auc_score(y[test], mod.decision_function(X[test, :])))
auc.append(metrics.balanced_accuracy_score(y[test], mod.predict(X[test, :])))
print("Test AUC:%.2f; bACC:%.2f" % (np.mean(bacc), np.mean(auc)))
Out:
Test AUC:0.86; bACC:0.80
cross_val_score(): single metric
scores = cross_val_score(estimator=mod, X=X, y=y, cv=5)
print("Test ACC:%.2f" % scores.mean())
Out:
Test ACC:0.80
Provide your own CV and score
def balanced_acc(estimator, X, y, **kwargs):
"""Balanced acuracy scorer."""
return metrics.recall_score(y, estimator.predict(X), average=None).mean()
scores = cross_val_score(estimator=mod, X=X, y=y, cv=cv,
scoring=balanced_acc)
print("Test bACC:%.2f" % scores.mean())
Out:
Test bACC:0.80
cross_validate(): multi metric, + time, etc.
from sklearn.model_selection import cross_validate
scores = cross_validate(estimator=mod, X=X, y=y, cv=cv,
scoring=['balanced_accuracy', 'roc_auc'])
print("Test AUC:%.2f; bACC:%.2f" % (scores['test_roc_auc'].mean(),
scores['test_balanced_accuracy'].mean()))
Out:
Test AUC:0.86; bACC:0.80
Cross-validation for model selection¶
Combine CV and grid search: Re-split (inner split) train set into CV folds train/validation folds and build a GridSearchCV out of it:
# Outer split:
X_train, X_test, y_train, y_test =\
train_test_split(X, y, test_size=0.25, shuffle=True, random_state=42)
cv_inner = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# Cross-validation for model selection
lm_cv = GridSearchCV(lm.LogisticRegression(), {'C': 10. ** np.arange(-3, 3)},
cv=cv_inner, n_jobs=5)
# Fit, indluding model selection with internal CV
lm_cv.fit(X_train, y_train)
# Predict
y_pred_test = lm_cv.predict(X_test)
print("Test bACC: %.2f" % metrics.balanced_accuracy_score(y_test, y_pred_test))
Out:
Test bACC: 0.63
Cross-validation for both model (outer) evaluation and model (inner) selection¶
cv_outer = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
cv_inner = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
# Cross-validation for model (inner) selection
lm_cv = GridSearchCV(lm.Ridge(), {'alpha': 10. ** np.arange(-3, 3)},
cv=cv_inner, n_jobs=5)
# Cross-validation for model (outer) evaluation
scores = cross_validate(estimator=mod, X=X, y=y, cv=cv_outer,
scoring=['balanced_accuracy', 'roc_auc'])
print("Test AUC:%.2f; bACC:%.2f, Time: %.2fs" % (scores['test_roc_auc'].mean(),
scores['test_balanced_accuracy'].mean(),
scores['fit_time'].sum()))
Out:
Test AUC:0.85; bACC:0.74, Time: 0.03s
Models with built-in cross-validation¶
Let sklearn select the best parameters over a default grid.
Classification
print("== Logistic Ridge (L2 penalty) ==")
mod_cv = lm.LogisticRegressionCV(class_weight='balanced', scoring='balanced_accuracy',
n_jobs=-1, cv=5)
scores = cross_val_score(estimator=mod_cv, X=X, y=y, cv=5)
print("Test ACC:%.2f" % scores.mean())
Out:
== Logistic Ridge (L2 penalty) ==
Test ACC:0.78
Regression
X, y, coef = datasets.make_regression(n_samples=50, n_features=100, noise=10,
n_informative=2, random_state=42, coef=True)
print("== Ridge (L2 penalty) ==")
model = lm.RidgeCV(cv=3)
scores = cross_val_score(estimator=model, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
print("== Lasso (L1 penalty) ==")
model = lm.LassoCV(n_jobs=-1, cv=3)
scores = cross_val_score(estimator=model, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
print("== ElasticNet (L1 penalty) ==")
model = lm.ElasticNetCV(l1_ratio=[.1, .5, .9], n_jobs=-1, cv=3)
scores = cross_val_score(estimator=model, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
Out:
== Ridge (L2 penalty) ==
Test r2:0.16
== Lasso (L1 penalty) ==
Test r2:0.74
== ElasticNet (L1 penalty) ==
Test r2:0.58
Random Permutations: sample the null distribution¶
A permutation test is a type of non-parametric randomization test in which the null distribution of a test statistic is estimated by randomly permuting the observations.
Permutation tests are highly attractive because they make no assumptions other than that the observations are independent and identically distributed under the null hypothesis.
Compute a observed statistic \(t_{obs}\) on the data.
Use randomization to compute the distribution of \(t\) under the null hypothesis: Perform \(N\) random permutation of the data. For each sample of permuted data, \(i\) the data compute the statistic \(t_i\). This procedure provides the distribution of t under the null hypothesis \(H_0\): \(P(t \vert H_0)\)
Compute the p-value = \(P(t>t_{obs} | H_0) \left\vert\{t_i > t_{obs}\}\right\vert\), where \(t_i's include :math:\).
Example Ridge regression
Sample the distributions of r-squared and coefficients of ridge regression under the null hypothesis. Simulated dataset:
# Regression dataset where first 2 features are predictives
np.random.seed(0)
n_features = 5
n_features_info = 2
n_samples = 100
X = np.random.randn(100, 5)
beta = np.zeros(n_features)
beta[:n_features_info] = 1
Xbeta = np.dot(X, beta)
eps = np.random.randn(n_samples)
y = Xbeta + eps
Random permutations¶
# Fit model on all data (!! risk of overfit)
model = lm.RidgeCV()
model.fit(X, y)
print("Coefficients on all data:")
print(model.coef_)
# Random permutation loop
nperm = 1000 # !! Should be at least 1000 (to assess a p-value at 1%)
scores_names = ["r2"]
scores_perm = np.zeros((nperm + 1, len(scores_names)))
coefs_perm = np.zeros((nperm + 1, X.shape[1]))
scores_perm[0, :] = metrics.r2_score(y, model.predict(X))
coefs_perm[0, :] = model.coef_
orig_all = np.arange(X.shape[0])
for perm_i in range(1, nperm + 1):
model.fit(X, np.random.permutation(y))
y_pred = model.predict(X).ravel()
scores_perm[perm_i, :] = metrics.r2_score(y, y_pred)
coefs_perm[perm_i, :] = model.coef_
# One-tailed empirical p-value
pval_pred_perm = np.sum(scores_perm >= scores_perm[0]) / scores_perm.shape[0]
pval_coef_perm = np.sum(coefs_perm >= coefs_perm[0, :], axis=0) / coefs_perm.shape[0]
print("R2 p-value: %.3f" % pval_pred_perm)
print("Coeficients p-values:", np.round(pval_coef_perm, 3))
Out:
Coefficients on all data:
[ 1.02 1.06 0.21 -0.02 -0.05]
R2 p-value: 0.001
Coeficients p-values: [0. 0. 0.1 0.57 0.63]
Compute p-values corrected for multiple comparisons using FWER max-T (Westfall and Young, 1993) procedure.
pval_coef_perm_tmax = np.array([np.sum(coefs_perm.max(axis=1) >= coefs_perm[0, j])
for j in range(coefs_perm.shape[1])]) / coefs_perm.shape[0]
print("P-values with FWER (Westfall and Young) correction")
print(pval_coef_perm_tmax)
Out:
P-values with FWER (Westfall and Young) correction
[0. 0. 0.41 0.98 0.99]
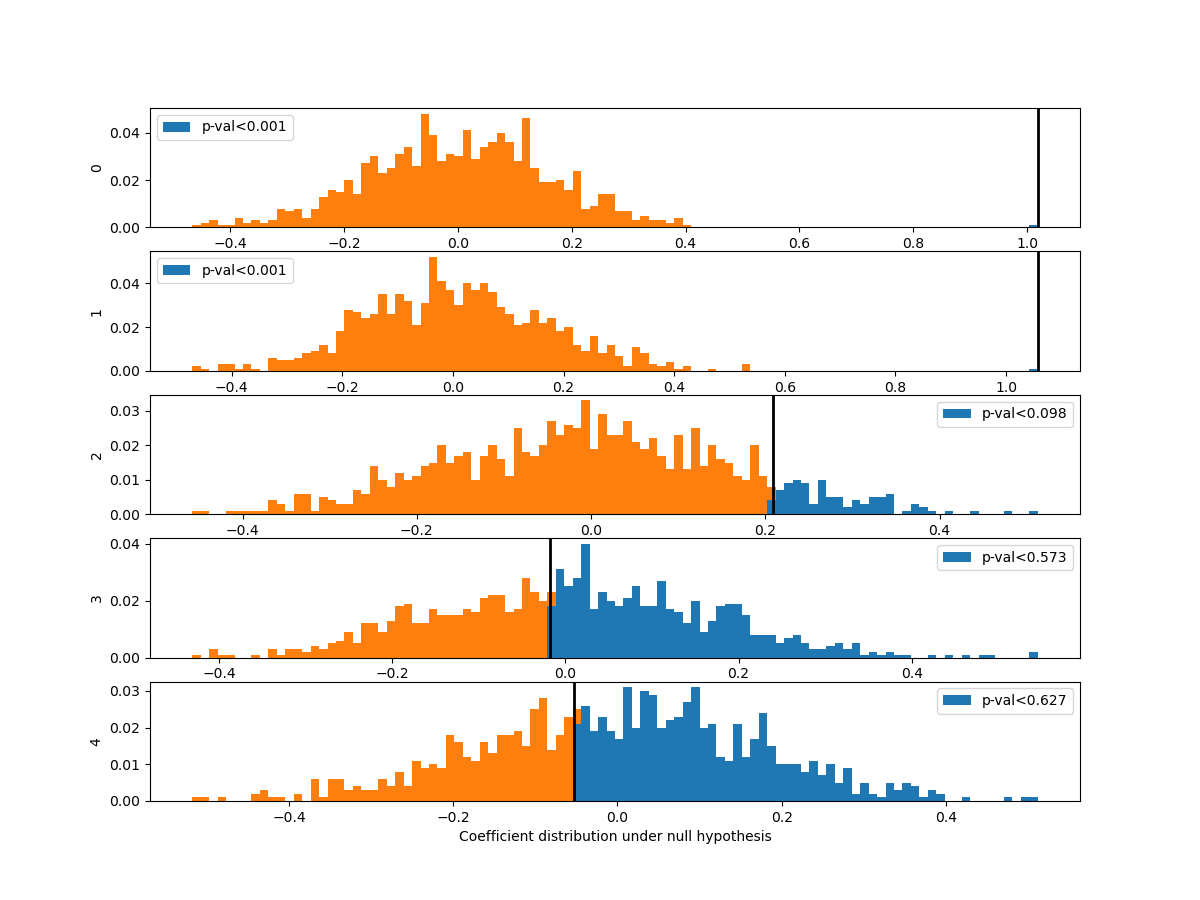
Plot distribution of third coefficient under null-hypothesis Coeffitients 0 and 1 are significantly different from 0.
def hist_pvalue(perms, ax, name):
"""Plot statistic distribution as histogram.
Paramters
---------
perms: 1d array, statistics under the null hypothesis.
perms[0] is the true statistic .
"""
# Re-weight to obtain distribution
pval = np.sum(perms >= perms[0]) / perms.shape[0]
weights = np.ones(perms.shape[0]) / perms.shape[0]
ax.hist([perms[perms >= perms[0]], perms], histtype='stepfilled',
bins=100, label="p-val<%.3f" % pval,
weights=[weights[perms >= perms[0]], weights])
ax.axvline(x=perms[0], color="k", linewidth=2)#, label="observed statistic")
ax.set_ylabel(name)
ax.legend()
return ax
n_coef = coefs_perm.shape[1]
fig, axes = plt.subplots(n_coef, 1, figsize=(12, 9))
for i in range(n_coef):
hist_pvalue( coefs_perm[:, i], axes[i], str(i))
_ = axes[-1].set_xlabel("Coefficient distribution under null hypothesis")
Exercise
Given the logistic regression presented above and its validation given a 5 folds CV.
Compute the p-value associated with the prediction accuracy measured with 5CV using a permutation test.
Compute the p-value associated with the prediction accuracy using a parametric test.
Bootstrapping¶
Bootstrapping is a statistical technique which consists in generating sample (called bootstrap samples) from an initial dataset of size N by randomly drawing with replacement N observations. It provides sub-samples with the same distribution than the original dataset. It aims to:
Assess the variability (standard error, [confidence intervals.](https://sebastianraschka.com/blog/2016/model-evaluation-selection-part2.html#the-bootstrap-method-and-empirical-confidence-intervals)) of performances scores or estimated parameters (see Efron et al. 1986).
Regularize model by fitting several models on bootstrap samples and averaging their predictions (see Baging and random-forest).
A great advantage of bootstrap is its simplicity. It is a straightforward way to derive estimates of standard errors and confidence intervals for complex estimators of complex parameters of the distribution, such as percentile points, proportions, odds ratio, and correlation coefficients.
Perform \(B\) sampling, with replacement, of the dataset.
For each sample \(i\) fit the model and compute the scores.
Assess standard errors and confidence intervals of scores using the scores obtained on the \(B\) resampled dataset. Or, average models predictions.
References:
[Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat Sci 1986;1:54–75](https://projecteuclid.org/download/pdf_1/euclid.ss/1177013815)
# Bootstrap loop
nboot = 100 # !! Should be at least 1000
scores_names = ["r2"]
scores_boot = np.zeros((nboot, len(scores_names)))
coefs_boot = np.zeros((nboot, X.shape[1]))
orig_all = np.arange(X.shape[0])
for boot_i in range(nboot):
boot_tr = np.random.choice(orig_all, size=len(orig_all), replace=True)
boot_te = np.setdiff1d(orig_all, boot_tr, assume_unique=False)
Xtr, ytr = X[boot_tr, :], y[boot_tr]
Xte, yte = X[boot_te, :], y[boot_te]
model.fit(Xtr, ytr)
y_pred = model.predict(Xte).ravel()
scores_boot[boot_i, :] = metrics.r2_score(yte, y_pred)
coefs_boot[boot_i, :] = model.coef_
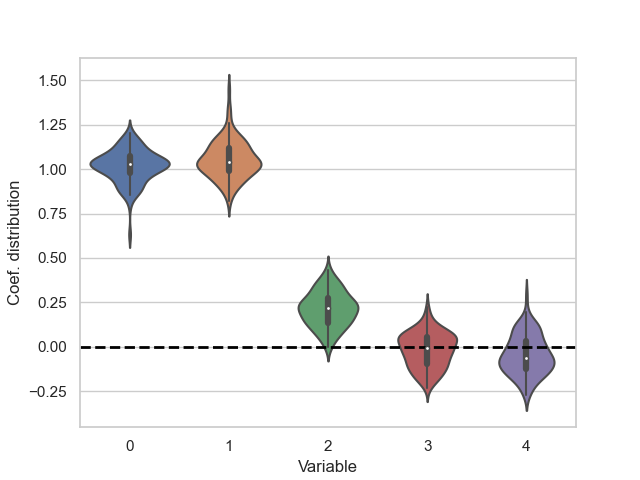
Compute Mean, SE, CI Coeffitients 0 and 1 are significantly different from 0.
scores_boot = pd.DataFrame(scores_boot, columns=scores_names)
scores_stat = scores_boot.describe(percentiles=[.975, .5, .025])
print("r-squared: Mean=%.2f, SE=%.2f, CI=(%.2f %.2f)" % tuple(scores_stat.loc[["mean", "std", "2.5%", "97.5%"], "r2"]))
coefs_boot = pd.DataFrame(coefs_boot)
coefs_stat = coefs_boot.describe(percentiles=[.975, .5, .025])
print("Coefficients distribution")
print(coefs_stat)
Out:
r-squared: Mean=0.59, SE=0.09, CI=(0.40 0.73)
Coefficients distribution
0 1 2 3 4
count 100.00 100.00 1.00e+02 100.00 100.00
mean 1.02 1.05 2.12e-01 -0.02 -0.05
std 0.09 0.11 9.75e-02 0.10 0.11
min 0.63 0.82 -2.69e-03 -0.23 -0.27
2.5% 0.86 0.88 3.27e-02 -0.20 -0.23
50% 1.03 1.04 2.17e-01 -0.01 -0.06
97.5% 1.17 1.29 3.93e-01 0.15 0.14
max 1.20 1.45 4.33e-01 0.22 0.29
Plot coefficient distribution
df = pd.DataFrame(coefs_boot)
staked = pd.melt(df, var_name="Variable", value_name="Coef. distribution")
sns.set_theme(style="whitegrid")
ax = sns.violinplot(x="Variable", y="Coef. distribution", data=staked)
_ = ax.axhline(0, ls='--', lw=2, color="black")
Parallel computation with joblib¶
Dataset
import numpy as np
from sklearn import datasets
import sklearn.linear_model as lm
import sklearn.metrics as metrics
from sklearn.model_selection import StratifiedKFold
X, y = datasets.make_classification(n_samples=20, n_features=5, n_informative=2, random_state=42)
cv = StratifiedKFold(n_splits=5)
Use cross_validate function
from sklearn.model_selection import cross_validate
estimator = lm.LogisticRegression(C=1, solver='lbfgs')
cv_results = cross_validate(estimator, X, y, cv=cv, n_jobs=5)
print(np.mean(cv_results['test_score']), cv_results['test_score'])
Out:
0.8 [0.5 0.5 1. 1. 1. ]
Sequential computation
If we want have full control of the operations performed within each fold (retrieve the models parameters, etc.). We would like to parallelize the folowing sequetial code:
# In[22]:
estimator = lm.LogisticRegression(C=1, solver='lbfgs')
y_test_pred_seq = np.zeros(len(y)) # Store predictions in the original order
coefs_seq = list()
for train, test in cv.split(X, y):
X_train, X_test, y_train, y_test = X[train, :], X[test, :], y[train], y[test]
estimator.fit(X_train, y_train)
y_test_pred_seq[test] = estimator.predict(X_test)
coefs_seq.append(estimator.coef_)
test_accs = [metrics.accuracy_score(y[test], y_test_pred_seq[test]) for train, test in cv.split(X, y)]
print(np.mean(test_accs), test_accs)
coefs_cv = np.array(coefs_seq)
print(coefs_cv)
print(coefs_cv.mean(axis=0))
print("Std Err of the coef")
print(coefs_cv.std(axis=0) / np.sqrt(coefs_cv.shape[0]))
Out:
0.8 [0.5, 0.5, 1.0, 1.0, 1.0]
[[[-0.88 0.63 1.19 -0.31 -0.38]]
[[-0.75 0.62 1.1 0.2 -0.4 ]]
[[-0.96 0.51 1.12 0.08 -0.26]]
[[-0.86 0.52 1.07 -0.11 -0.29]]
[[-0.9 0.51 1.09 -0.25 -0.28]]]
[[-0.87 0.56 1.11 -0.08 -0.32]]
Std Err of the coef
[[0.03 0.02 0.02 0.09 0.03]]
Parallel computation with joblib¶
from joblib import Parallel, delayed
from sklearn.base import is_classifier, clone
def _split_fit_predict(estimator, X, y, train, test):
X_train, X_test, y_train, y_test = X[train, :], X[test, :], y[train], y[test]
estimator.fit(X_train, y_train)
return [estimator.predict(X_test), estimator.coef_]
estimator = lm.LogisticRegression(C=1, solver='lbfgs')
parallel = Parallel(n_jobs=5)
cv_ret = parallel(
delayed(_split_fit_predict)(
clone(estimator), X, y, train, test)
for train, test in cv.split(X, y))
y_test_pred_cv, coefs_cv = zip(*cv_ret)
# Retrieve predictions in the original order
y_test_pred = np.zeros(len(y))
for i, (train, test) in enumerate(cv.split(X, y)):
y_test_pred[test] = y_test_pred_cv[i]
test_accs = [metrics.accuracy_score(y[test], y_test_pred[test]) for train, test in cv.split(X, y)]
print(np.mean(test_accs), test_accs)
Out:
0.8 [0.5, 0.5, 1.0, 1.0, 1.0]
Test same predictions and same coeficients
assert np.all(y_test_pred == y_test_pred_seq)
assert np.allclose(np.array(coefs_cv).squeeze(), np.array(coefs_seq).squeeze())
Total running time of the script: ( 0 minutes 4.727 seconds)