Resampling methods¶
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
Train, Validation and Test Sets¶
Machine learning algorithms overfit taining data. Predictive performances MUST be evaluated on independant hold-out dataset.
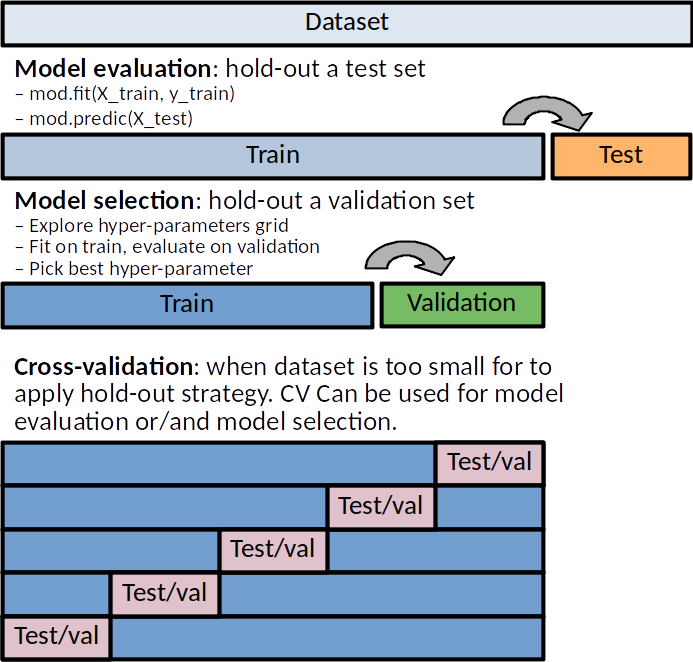
Train, validation and test sets.¶
Training dataset: Dataset used to fit the model (set the model parameters like weights). The training error can be easily calculated by applying the statistical learning method to the observations used in its training. But because of overfitting, the training error rate can dramatically underestimate the error that would be obtained on new samples.
Validation dataset: Dataset used to provide an unbiased evaluation of a model fit on the training dataset while tuning model hyperparameters, ie. Model selection. The validation error is the average error that results from a learning method to predict the response on a new (validation) samples that is, on samples that were not used in training the method.
Test dataset: Dataset used to provide an unbiased evaluation of a final model fitted on the training dataset. It is only used once a model is completely trained(using the train and validation sets).
What is the Difference Between Test and Validation Datasets? by Jason Brownlee
Thus the original dataset is generally split in a training, validation and a test data sets. Large training+validation set (80%) small test set (20%) might provide a poor estimation of the predictive performances (same argument stands for train vs validation samples). On the contrary, large test set and small training set might produce a poorly estimated learner. This is why, on situation where we cannot afford such split, cross-validation scheme can be use for model selection or/and for model evaluation.
If sample size is limited, train/validation/test split may not be possible. Cross Validation (CV) (see below) can be used to replace:
Outer (train/test) split of model evaluation.
Inner train/validation split of model selection (more frequent situation).
Inner and outer splits, leading to two nested CV.
import numpy as np
from sklearn import datasets
import sklearn.linear_model as lm
from sklearn.model_selection import train_test_split, KFold, PredefinedSplit
from sklearn.model_selection import cross_val_score, GridSearchCV
import sklearn.metrics as metrics
X, y = datasets.make_regression(n_samples=100, n_features=100,
n_informative=10, random_state=42)
1. Split dataset in train/test sets for model (outer) evaluation¶
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
1.1 Predefined train/validation split for model (inner) selection¶
Re-split train set into train/validation and build a CV object (inner split) out of it:
train_idx, validation_idx = train_test_split(np.arange(X_train.shape[0]),
test_size=0.25, random_state=42)
split_inner = PredefinedSplit(test_fold=validation_idx)
print("Train set size: %i" % X_train[train_idx].shape[0])
print("Validation set size: %i" % X_train[validation_idx].shape[0])
print("Test set size: %i" % X_test.shape[0])
lm_cv = GridSearchCV(lm.Ridge(), {'alpha': 10. ** np.arange(-3, 3)},
cv=split_inner, n_jobs=5)
# Fit, indluding model selection with internal Train/validation split
lm_cv.fit(X_train, y_train)
# Predict
y_pred_test = lm_cv.predict(X_test)
print("Test R2: %.2f" % metrics.r2_score(y_test, y_pred_test))
Train set size: 56
Validation set size: 19
Test set size: 25
Test R2: 0.80
1.2 Cross-validation for model (inner) selection¶
cv_inner = KFold(n_splits=5, shuffle=True, random_state=42)
print("Train/Validation set sizes: ",
[[len(tr), len(ev)] for tr, ev in cv_inner.split(X_train)])
print("Test set size: %i" % X_test.shape[0])
# Cross-validation for model selection
lm_cv = GridSearchCV(lm.Ridge(), {'alpha': 10. ** np.arange(-3, 3)},
cv=cv_inner, n_jobs=5)
# Fit, indluding model selection with internal CV
lm_cv.fit(X_train, y_train)
# Predict
y_pred_test = lm_cv.predict(X_test)
print("Test R2: %.2f" % metrics.r2_score(y_test, y_pred_test))
Train/Validation set sizes: [[60, 15], [60, 15], [60, 15], [60, 15], [60, 15]]
Test set size: 25
Test R2: 0.80
2. Cross-validation for both model (outer) evaluation and model (inner) selection¶
cv_outer = KFold(n_splits=5, shuffle=True, random_state=42)
sizes = pd.DataFrame([[len(train), len(eva), len(test)]
for tr_outer, test in cv_outer.split(X)
for train, eva in cv_inner.split(X[tr_outer])
], columns=["train", 'validation', 'test'])
print("Train/Validation set sizes: ")
print(sizes.iloc[np.r_[0:4, -4:0]])
print("Nb runs: %i (nb outer folds x nb inner folds)" % sizes.shape[0])
# Cross-validation for model (inner) selection
lm_cv = GridSearchCV(lm.Ridge(), {'alpha': 10. ** np.arange(-3, 3)}, cv=cv_inner, n_jobs=5)
# Cross-validation for model (outer) evaluation
scores = cross_val_score(estimator=lm_cv, X=X, y=y, cv=cv_outer)
print("CV R2:%.2f" % scores.mean())
Train/Validation set sizes:
train validation test
0 64 16 20
1 64 16 20
2 64 16 20
3 64 16 20
21 64 16 20
22 64 16 20
23 64 16 20
24 64 16 20
Nb runs: 25 (nb outer folds x nb inner folds)
CV R2:0.70
Cross-Validation (CV)¶
Cross-Validation scheme randomly divides the set of observations into \(K\) groups, or folds, of approximately equal size. The first fold is treated as a validation set, and the method \(f()\) is fitted on the remaining union of \(K - 1\) folds: (\(f(\boldsymbol{X}_{-K}, \boldsymbol{y}_{-K})\)).
The measure of performance (the score function \(\mathcal{S}\)), either a error measure or an correct prediction measure is an average of a loss error or correct prediction measure, noted \(\mathcal{L}\), between a true target value and the predicted target value. The score function is evaluated of the on the observations in the held-out fold. For each sample \(i\) we consider the model estimated \(f(\boldsymbol{X}_{-k(i)}, \boldsymbol{y}_{-k(i)}\) on the data set without the group \(k\) that contains \(i\) noted \(-k(i)\). This procedure is repeated \(K\) times; each time, a different group of observations is treated as a test set. Then we compare the predicted value (\(f_{-k(i)}(\boldsymbol{x}_i) = \hat{y_i})\) with true value \(y_i\) using a Error or Loss function \(\mathcal{L}(y, \hat{y})\).
For 10-fold we can either average over 10 values (Macro measure) or concatenate the 10 experiments and compute the micro measures.
Two strategies micro vs macro estimates:
Micro measure: average(individual scores): compute a score \(\mathcal{S}\) for each sample and average over all samples. It is simillar to average score(concatenation): an averaged score computed over all concatenated samples.
Macro measure mean(CV scores) (the most commonly used method): compute a score \(\mathcal{S}\) on each each fold \(k\) and average accross folds:
These two measures (an average of average vs. a global average) are generaly similar. They may differ slightly is folds are of different sizes.
This validation scheme is known as the K-Fold CV. Typical choices of \(K\) are 5 or 10, [Kohavi 1995]. The extreme case where \(K = N\) is known as leave-one-out cross-validation, LOO-CV.
Usually the error function \(\mathcal{L}()\) is the r-squared score. However other function could be used.
import numpy as np
import sklearn.metrics as metrics
from sklearn.model_selection import KFold
estimator = lm.Ridge(alpha=10)
cv = KFold(n_splits=5, random_state=42)
r2_train, r2_test = list(), list()
for train, test in cv.split(X):
estimator.fit(X[train, :], y[train])
r2_train.append(metrics.r2_score(y[train], estimator.predict(X[train, :])))
r2_test.append(metrics.r2_score(y[test], estimator.predict(X[test, :])))
print("Train r2:%.2f" % np.mean(r2_train))
print("Test r2:%.2f" % np.mean(r2_test))
Train r2:0.99
Test r2:0.73
Scikit-learn provides user-friendly function to perform CV:
from sklearn.model_selection import cross_val_score
scores = cross_val_score(estimator=estimator, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
# provide a cv
cv = KFold(n_splits=5, random_state=42)
scores = cross_val_score(estimator=estimator, X=X, y=y, cv=cv)
print("Test r2:%.2f" % scores.mean())
Test r2:0.73
Test r2:0.73
With classification problems it is essential to sample folds where each
set contains approximately the same percentage of samples of each target
class as the complete set. This is called stratification. In this
case, we will use StratifiedKFold with is a variation of k-fold
which returns stratified folds.
Usually the error function \(L()\) are, at least, the sensitivity and the specificity. However other function could be used.
import numpy as np
from sklearn import datasets
import sklearn.linear_model as lm
import sklearn.metrics as metrics
from sklearn.model_selection import StratifiedKFold
X, y = datasets.make_classification(n_samples=100, n_features=100,
n_informative=10, random_state=42)
estimator = lm.LogisticRegression(C=1, solver='lbfgs')
cv = StratifiedKFold(n_splits=5)
# Lists to store scores by folds (for macro measure only)
recalls_train, recalls_test, acc_test = list(), list(), list()
# Or vector of test predictions (for both macro and micro measures, not for training samples)
y_test_pred = np.zeros(len(y))
for train, test in cv.split(X, y):
estimator.fit(X[train, :], y[train])
recalls_train.append(metrics.recall_score(y[train], estimator.predict(X[train, :]), average=None))
recalls_test.append(metrics.recall_score(y[test], estimator.predict(X[test, :]), average=None))
acc_test.append(metrics.accuracy_score(y[test], estimator.predict(X[test, :])))
# Store test predictions (for micro measures)
y_test_pred[test] = estimator.predict(X[test, :])
print("== Macro measures ==")
# Use lists of scores
recalls_train = np.array(recalls_train)
recalls_test = np.array(recalls_test)
print("Train SPC:%.2f; SEN:%.2f" % tuple(recalls_train.mean(axis=0)))
print("Test SPC:%.2f; SEN:%.2f" % tuple(recalls_test.mean(axis=0)), )
print("Test ACC:%.2f, ballanced ACC:%.2f" %
(np.mean(acc_test), recalls_test.mean(axis=1).mean()), "Folds:", acc_test)
# Or use vector to test predictions
acc_test = [metrics.accuracy_score(y[test], y_test_pred[test]) for train, test in cv.split(X, y)]
print("Test ACC:%.2f" % np.mean(acc_test), "Folds:", acc_test)
print("== Micro measures ==")
print("Test SPC:%.2f; SEN:%.2f" % \
tuple(metrics.recall_score(y, y_test_pred, average=None)))
print("Test ACC:%.2f" % metrics.accuracy_score(y, y_test_pred))
== Macro measures ==
Train SPC:1.00; SEN:1.00
Test SPC:0.78; SEN:0.82
Test ACC:0.80, ballanced ACC:0.80 Folds: [0.9, 0.7, 0.95, 0.7, 0.75]
Test ACC:0.80 Folds: [0.9, 0.7, 0.95, 0.7, 0.75]
== Micro measures ==
Test SPC:0.78; SEN:0.82
Test ACC:0.80
Scikit-learn provides user-friendly function to perform CV:
from sklearn.model_selection import cross_val_score
scores = cross_val_score(estimator=estimator, X=X, y=y, cv=5)
scores.mean()
# provide CV and score
def balanced_acc(estimator, X, y, **kwargs):
'''
Balanced acuracy scorer
'''
return metrics.recall_score(y, estimator.predict(X), average=None).mean()
scores = cross_val_score(estimator=estimator, X=X, y=y, cv=5, scoring=balanced_acc)
print("Test ACC:%.2f" % scores.mean())
Test ACC:0.80
Note that with Scikit-learn user-friendly function we average the scores’ average obtained on individual folds which may provide slightly different results that the overall average presented earlier.
Parallel computation with joblib¶
Dataset
import numpy as np
from sklearn import datasets
import sklearn.linear_model as lm
import sklearn.metrics as metrics
from sklearn.model_selection import StratifiedKFold
X, y = datasets.make_classification(n_samples=20, n_features=5, n_informative=2, random_state=42)
cv = StratifiedKFold(n_splits=5)
from sklearn.model_selection import cross_validate
estimator = lm.LogisticRegression(C=1, solver='lbfgs')
cv_results = cross_validate(estimator, X, y, cv=cv, n_jobs=5)
print(np.mean(cv_results['test_score']), cv_results['test_score'])
0.8 [0.5 0.5 1. 1. 1. ]
### Sequential computation
If we want have full control of the operations performed within each fold (retrieve the models parameters, etc.). We would like to parallelize the folowing sequetial code:
estimator = lm.LogisticRegression(C=1, solver='lbfgs')
y_test_pred_seq = np.zeros(len(y)) # Store predictions in the original order
coefs_seq = list()
for train, test in cv.split(X, y):
X_train, X_test, y_train, y_test = X[train, :], X[test, :], y[train], y[test]
estimator.fit(X_train, y_train)
y_test_pred_seq[test] = estimator.predict(X_test)
coefs_seq.append(estimator.coef_)
test_accs = [metrics.accuracy_score(y[test], y_test_pred_seq[test]) for train, test in cv.split(X, y)]
print(np.mean(test_accs), test_accs)
coefs_cv = np.array(coefs_seq)
print(coefs_cv)
print(coefs_cv.mean(axis=0))
print("Std Err of the coef")
print(coefs_cv.std(axis=0) / np.sqrt(coefs_cv.shape[0]))
0.8 [0.5, 0.5, 1.0, 1.0, 1.0]
[[[-0.87692513 0.6260013 1.18714373 -0.30685978 -0.38037393]]
[[-0.7464993 0.62138165 1.10144804 0.19800115 -0.40112109]]
[[-0.96020317 0.51135134 1.1210943 0.08039112 -0.2643663 ]]
[[-0.85755505 0.52010552 1.06637346 -0.10994258 -0.29152132]]
[[-0.89914467 0.51481483 1.08675378 -0.24767837 -0.27899525]]]
[[-0.86806546 0.55873093 1.11256266 -0.07721769 -0.32327558]]
Std Err of the coef
[[0.03125544 0.02376198 0.01850211 0.08566194 0.02510739]]
from joblib import Parallel, delayed
from sklearn.base import is_classifier, clone
def _split_fit_predict(estimator, X, y, train, test):
X_train, X_test, y_train, y_test = X[train, :], X[test, :], y[train], y[test]
estimator.fit(X_train, y_train)
return [estimator.predict(X_test), estimator.coef_]
estimator = lm.LogisticRegression(C=1, solver='lbfgs')
parallel = Parallel(n_jobs=5)
cv_ret = parallel(
delayed(_split_fit_predict)(
clone(estimator), X, y, train, test)
for train, test in cv.split(X, y))
y_test_pred_cv, coefs_cv = zip(*cv_ret)
# Retrieve predictions in the original order
y_test_pred = np.zeros(len(y))
for i, (train, test) in enumerate(cv.split(X, y)):
y_test_pred[test] = y_test_pred_cv[i]
test_accs = [metrics.accuracy_score(y[test], y_test_pred[test]) for train, test in cv.split(X, y)]
print(np.mean(test_accs), test_accs)
0.8 [0.5, 0.5, 1.0, 1.0, 1.0]
Test same predictions and same coeficients
assert np.all(y_test_pred == y_test_pred_seq)
assert np.allclose(np.array(coefs_cv).squeeze(), np.array(coefs_seq).squeeze())
CV for model selection: setting the hyper parameters¶
It is important to note CV may be used for two separate goals:
Model assessment: having chosen a final model, estimating its prediction error (generalization error) on new data.
Model selection: estimating the performance of different models in order to choose the best one. One special case of model selection is the selection model’s hyper parameters. Indeed remember that most of learning algorithm have a hyper parameters (typically the regularization parameter) that has to be set.
Generally we must address the two problems simultaneously. The usual approach for both problems is to randomly divide the dataset into three parts: a training set, a validation set, and a test set.
The training set (train) is used to fit the models;
the validation set (val) is used to estimate prediction error for model selection or to determine the hyper parameters over a grid of possible values.
the test set (test) is used for assessment of the generalization error of the final chosen model.
Model selection of the best hyper parameters over a grid of possible values
For each possible values of hyper parameters \(\alpha_k\):
Fit the learner on training set: \(f(X_{train}, y_{train}, \alpha_k)\)
Evaluate the model on the validation set and keep the parameter(s) that minimises the error measure
\(\alpha_* = \arg \min L(f(X_{train}), y_{val}, \alpha_k)\)
Refit the learner on all training + validation data using the best hyper parameters: \(f^* \equiv f(X_{train \cup val}, y_{train \cup val}, \alpha_*)\)
** Model assessment ** of \(f^*\) on the test set: \(L(f^*(X_{test}), y_{test})\)
Most of time, we cannot afford such three-way split. Thus, again we will use CV, but in this case we need two nested CVs.
One outer CV loop, for model assessment. This CV performs \(K\) splits of the dataset into training plus validation (\(X_{-K}, y_{-K}\)) set and a test set \(X_{K}, y_{K}\)
One inner CV loop, for model selection. For each run of the outer loop, the inner loop loop performs \(L\) splits of dataset (\(X_{-K}, y_{-K}\)) into training set: (\(X_{-K,-L}, y_{-K,-L}\)) and a validation set: (\(X_{-K,L}, y_{-K,L}\)).
Note that the inner CV loop combined with the learner form a new learner
with an automatic model (parameter) selection procedure. This new
learner can be easily constructed using Scikit-learn. The learned is
wrapped inside a GridSearchCV class.
Then the new learned can be plugged into the classical outer CV loop.
import numpy as np
from sklearn import datasets
import sklearn.linear_model as lm
from sklearn.model_selection import GridSearchCV
import sklearn.metrics as metrics
from sklearn.model_selection import KFold
# Dataset
noise_sd = 10
X, y, coef = datasets.make_regression(n_samples=50, n_features=100, noise=noise_sd,
n_informative=2, random_state=42, coef=True)
# Use this to tune the noise parameter such that snr < 5
print("SNR:", np.std(np.dot(X, coef)) / noise_sd)
# param grid over alpha & l1_ratio
param_grid = {'alpha': 10. ** np.arange(-3, 3), 'l1_ratio':[.1, .5, .9]}
# Warp
model = GridSearchCV(lm.ElasticNet(max_iter=10000), param_grid, cv=5)
SNR: 2.6358469446381614
Sklearn will automatically select a grid of parameters, most of time use the defaults values.
n_jobs is the number of CPUs to use during the cross validation. If
-1, use all the CPUs.
Biased usage: fit on all data, ommit outer CV loop
model.fit(X, y)
print("Train r2:%.2f" % metrics.r2_score(y, model.predict(X)))
print(model.best_params_)
Train r2:0.96
{'alpha': 1.0, 'l1_ratio': 0.9}
User made outer CV, useful to extract specific information
cv = KFold(n_splits=5, random_state=42)
r2_train, r2_test = list(), list()
alphas = list()
for train, test in cv.split(X, y):
X_train, X_test, y_train, y_test = X[train, :], X[test, :], y[train], y[test]
model.fit(X_train, y_train)
r2_test.append(metrics.r2_score(y_test, model.predict(X_test)))
r2_train.append(metrics.r2_score(y_train, model.predict(X_train)))
alphas.append(model.best_params_)
print("Train r2:%.2f" % np.mean(r2_train))
print("Test r2:%.2f" % np.mean(r2_test))
print("Selected alphas:", alphas)
Train r2:1.00
Test r2:0.55
Selected alphas: [{'alpha': 0.001, 'l1_ratio': 0.9}, {'alpha': 0.001, 'l1_ratio': 0.9}, {'alpha': 0.001, 'l1_ratio': 0.9}, {'alpha': 0.01, 'l1_ratio': 0.9}, {'alpha': 0.001, 'l1_ratio': 0.9}]
User-friendly sklearn for outer CV
from sklearn.model_selection import cross_val_score
scores = cross_val_score(estimator=model, X=X, y=y, cv=cv)
print("Test r2:%.2f" % scores.mean())
Test r2:0.55
from sklearn import datasets
import sklearn.linear_model as lm
import sklearn.metrics as metrics
from sklearn.model_selection import cross_val_score
# Dataset
X, y, coef = datasets.make_regression(n_samples=50, n_features=100, noise=10,
n_informative=2, random_state=42, coef=True)
print("== Ridge (L2 penalty) ==")
model = lm.RidgeCV(cv=3)
# Let sklearn select a list of alphas with default LOO-CV
scores = cross_val_score(estimator=model, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
print("== Lasso (L1 penalty) ==")
model = lm.LassoCV(n_jobs=-1, cv=3)
# Let sklearn select a list of alphas with default 3CV
scores = cross_val_score(estimator=model, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
print("== ElasticNet (L1 penalty) ==")
model = lm.ElasticNetCV(l1_ratio=[.1, .5, .9], n_jobs=-1, cv=3)
# Let sklearn select a list of alphas with default 3CV
scores = cross_val_score(estimator=model, X=X, y=y, cv=5)
print("Test r2:%.2f" % scores.mean())
== Ridge (L2 penalty) ==
Test r2:0.16
== Lasso (L1 penalty) ==
Test r2:0.74
== ElasticNet (L1 penalty) ==
Test r2:0.58
from sklearn import datasets
import sklearn.linear_model as lm
import sklearn.metrics as metrics
from sklearn.model_selection import cross_val_score
X, y = datasets.make_classification(n_samples=100, n_features=100,
n_informative=10, random_state=42)
# provide CV and score
def balanced_acc(estimator, X, y, **kwargs):
'''
Balanced accuracy scorer
'''
return metrics.recall_score(y, estimator.predict(X), average=None).mean()
print("== Logistic Ridge (L2 penalty) ==")
model = lm.LogisticRegressionCV(class_weight='balanced', scoring=balanced_acc, n_jobs=-1, cv=3)
# Let sklearn select a list of alphas with default LOO-CV
scores = cross_val_score(estimator=model, X=X, y=y, cv=5)
print("Test ACC:%.2f" % scores.mean())
== Logistic Ridge (L2 penalty) ==
Test ACC:0.76
Random Permutations: sample the null distribution¶
A permutation test is a type of non-parametric randomization test in which the null distribution of a test statistic is estimated by randomly permuting the observations.
Permutation tests are highly attractive because they make no assumptions other than that the observations are independent and identically distributed under the null hypothesis.
Compute a observed statistic \(t_{obs}\) on the data.
Use randomization to compute the distribution of \(t\) under the null hypothesis: Perform \(N\) random permutation of the data. For each sample of permuted data, \(i\) the data compute the statistic \(t_i\). This procedure provides the distribution of \(t\) under the null hypothesis \(H_0\): \(P(t \vert H_0)\)
Compute the p-value = \(P(t>t_{obs} | H_0) \left\vert\{t_i > t_{obs}\}\right\vert\), where \(t_i\)’s include \(t_{obs}\).
Sample the distributions of r-squared and coefficients of ridge regression under the null hypothesis. Simulated dataset:
import numpy as np
import sklearn.linear_model as lm
import sklearn.metrics as metrics
import pandas as pd
# Regression dataset
np.random.seed(0)
n_features = 5
n_features_info = 2
n_samples = 100
X = np.random.randn(n_samples, n_features)
beta = np.zeros(n_features)
beta[:n_features_info] = 1
Xbeta = np.dot(X, beta)
eps = np.random.randn(n_samples)
y = Xbeta + eps
Random permutations
# Fit model on all data (!! risk of overfit)
model = lm.RidgeCV()
model.fit(X, y)
print("Coefficients on all data:")
print(model.coef_)
# Random permutation loop
nperm = 1000 # !! Should be at least 1000 (to assess a p-value at 1%)
scores_names = ["r2"]
scores_perm = np.zeros((nperm + 1, len(scores_names)))
coefs_perm = np.zeros((nperm + 1, X.shape[1]))
scores_perm[0, :] = metrics.r2_score(y, model.predict(X))
coefs_perm[0, :] = model.coef_
orig_all = np.arange(X.shape[0])
for perm_i in range(1, nperm + 1):
model.fit(X, np.random.permutation(y))
y_pred = model.predict(X).ravel()
scores_perm[perm_i, :] = metrics.r2_score(y, y_pred)
coefs_perm[perm_i, :] = model.coef_
# One-tailed empirical p-value
pval_pred_perm = np.sum(scores_perm >= scores_perm[0]) / scores_perm.shape[0]
pval_coef_perm = np.sum(coefs_perm >= coefs_perm[0, :], axis=0) / coefs_perm.shape[0]
print("R2 p-value: %.3f" % pval_pred_perm)
print("Coeficients p-values:", np.round(pval_coef_perm, 3))
Coefficients on all data:
[ 1.01872179 1.05713711 0.20873888 -0.01784094 -0.05265821]
R2 p-value: 0.001
Coeficients p-values: [0.001 0.001 0.098 0.573 0.627]
Compute p-values corrected for multiple comparisons using max-T (Westfall and Young, 1993) FWER
pval_coef_perm_tmax = np.array([np.sum(coefs_perm.max(axis=1) >= coefs_perm[0, j])
for j in range(coefs_perm.shape[1])]) / coefs_perm.shape[0]
print("P-values with FWER (Westfall and Young) correction")
print(pval_coef_perm_tmax)
P-values with FWER (Westfall and Young) correction
[0.000999 0.000999 0.41058941 0.98001998 0.99200799]
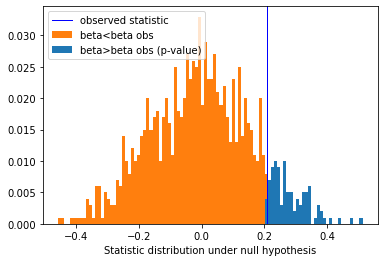
# Plot distribution of third coefficient under null-hypothesis
perms = coefs_perm[:, 2]
# Re-weight to obtain distribution
weights = np.ones(perms.shape[0]) / perms.shape[0]
plt.hist([perms[perms >= perms[0]], perms], histtype='stepfilled',
bins=100, label=["beta>beta obs (p-value)", "beta<beta obs"],
weights=[weights[perms >= perms[0]], weights])
plt.xlabel("Statistic distribution under null hypothesis")
plt.axvline(x=perms[0], color='blue', linewidth=1, label="observed statistic")
_ = plt.legend(loc="upper left")
Given the logistic regression presented above and its validation given a 5 folds CV.
Compute the p-value associated with the prediction accuracy measured with 5CV using a permutation test.
Compute the p-value associated with the prediction accuracy using a parametric test.
Bootstrapping¶
Bootstrapping is a statistical technique which consists in generating sample (called bootstrap samples) from an initial dataset of size \(N\) by randomly drawing with replacement \(N\) observations. It provides sub-samples with the same distribution than the original dataset. It aims to:
Assess the variability (standard error, confidence intervals.) of performances scores or estimated parameters (see Efron et al. 1986).
Regularize model by fitting several models on bootstrap samples and averaging their predictions (see Baging and random-forest).
A great advantage of bootstrap is its simplicity. It is a straightforward way to derive estimates of standard errors and confidence intervals for complex estimators of complex parameters of the distribution, such as percentile points, proportions, odds ratio, and correlation coefficients.
Perform \(B\) sampling, with replacement, of the dataset.
For each sample \(i\) fit the model and compute the scores.
Assess standard errors and confidence intervals of scores using the scores obtained on the \(B\) resampled dataset. Or, average models predictions.
References:
import pandas as pd
# Bootstrap loop
nboot = 100 # !! Should be at least 1000
scores_names = ["r2"]
scores_boot = np.zeros((nboot, len(scores_names)))
coefs_boot = np.zeros((nboot, X.shape[1]))
orig_all = np.arange(X.shape[0])
for boot_i in range(nboot):
boot_tr = np.random.choice(orig_all, size=len(orig_all), replace=True)
boot_te = np.setdiff1d(orig_all, boot_tr, assume_unique=False)
Xtr, ytr = X[boot_tr, :], y[boot_tr]
Xte, yte = X[boot_te, :], y[boot_te]
model.fit(Xtr, ytr)
y_pred = model.predict(Xte).ravel()
scores_boot[boot_i, :] = metrics.r2_score(yte, y_pred)
coefs_boot[boot_i, :] = model.coef_
# Compute Mean, SE, CI
scores_boot = pd.DataFrame(scores_boot, columns=scores_names)
scores_stat = scores_boot.describe(percentiles=[.975, .5, .025])
print("r-squared: Mean=%.2f, SE=%.2f, CI=(%.2f %.2f)" %\
tuple(scores_stat.loc[["mean", "std", "2.5%", "97.5%"], "r2"]))
coefs_boot = pd.DataFrame(coefs_boot)
coefs_stat = coefs_boot.describe(percentiles=[.975, .5, .025])
print("Coefficients distribution")
print(coefs_stat)
r-squared: Mean=0.59, SE=0.09, CI=(0.40 0.73)
Coefficients distribution
0 1 2 3 4
count 100.000000 100.000000 100.000000 100.000000 100.000000
mean 1.017598 1.053832 0.212464 -0.018828 -0.045851
std 0.091508 0.105196 0.097532 0.097343 0.110555
min 0.631917 0.819190 -0.002689 -0.231580 -0.270810
2.5% 0.857418 0.883319 0.032672 -0.195018 -0.233241
50% 1.027161 1.038053 0.216531 -0.010023 -0.063331
97.5% 1.174707 1.289990 0.392701 0.150340 0.141587
max 1.204006 1.449672 0.432764 0.220711 0.290928
Plot mean / CI